Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(HC-HB=9\Rightarrow HC=HB+9\)
Áp dụng hệ thức lượng:
\(AH^2=HB.HC\Leftrightarrow6^2=HB\left(HB+9\right)\)
\(\Leftrightarrow HB^2+9HB-36=0\Rightarrow\left[{}\begin{matrix}HB=3\\HB=-12\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow HC=HB+9=12\)
Ta có: HC-HB=9
nên HC=9+HB
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB^2+9HB-36=0\)
\(\Leftrightarrow\left(HB+12\right)\left(HB-3\right)=0\)
\(\Leftrightarrow HB=3\left(cm\right)\)
\(\Leftrightarrow HC=12\left(cm\right)\)

Đặt BC=x \(\Rightarrow\)BH=x-16
\(\Rightarrow\)AB2=x(x-16) \(\Leftrightarrow\)152=x(x-16) \(\Leftrightarrow\)x=25
\(\Rightarrow\)BC=25(cm),BH=25-16=9(cm)
AC=\(\sqrt{BC^2-AB^2}\)=20(cm)
AH=\(\sqrt{BH.HC}\)=12(cm

Ta có : \(BC=BH+CH=9+16=25\left(cm\right)\)
Áp dụng hệ thức lượng ta có :
+) \(AB^2=BH.BC\)
\(\Leftrightarrow AB^2=9\times25\)
\(\Leftrightarrow AB=\sqrt{225}=15\left(cm\right)\)
+) \(AC^2=HC.BC\)
\(\Leftrightarrow AC^2=16\times25\)
\(\Leftrightarrow AC=\sqrt{400}=20\left(cm\right)\)
Vậy ...
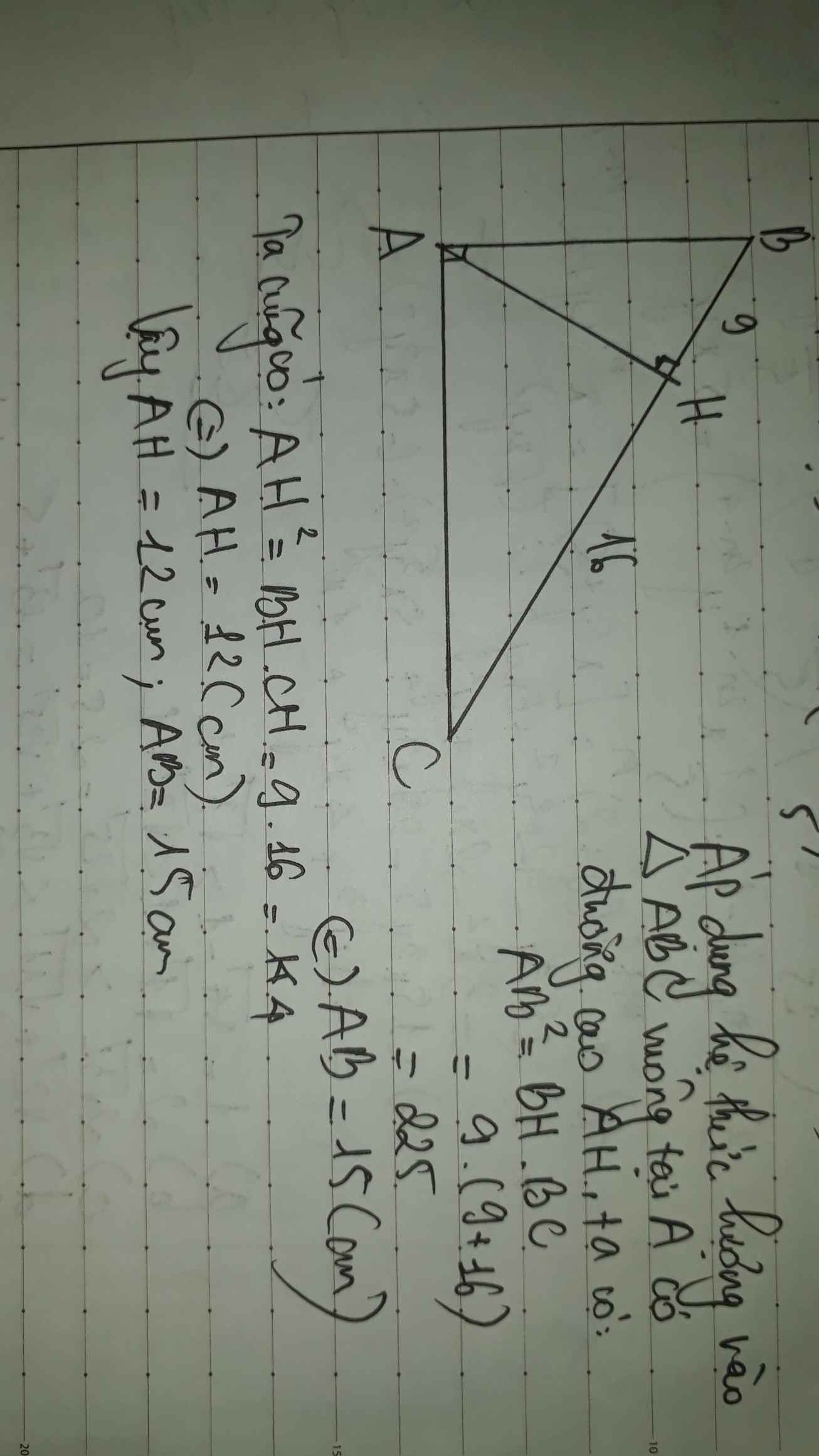
Áp dụng HTL trong tam giác ABC vuông tại A có đường cao AH:
\(AH^2=HB.HC\)
\(\Rightarrow AH=\sqrt{HB.HC}=\sqrt{9.16}=12\left(cm\right)\)
Hệ thức lượng hay hệ tích lượng vậy ạ :v