Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tam giác BHA và tam giác BCA là 2 tam giác vuông có:
+ góc BHA= góc BAC
=> tam giác BAH đồng dạng với BCA

a, Xét \(\Delta\)BAH và \(\Delta\)BCA có: \(\widehat{ABC}\) chung; \(\widehat{AHB}\) = \(\widehat{BAC}\) = 900
⇒\(\Delta\)BAH \(\sim\)\(\Delta\)BCA (g-g)
⇒\(\dfrac{BA}{BC}=\dfrac{AH}{CA}=\dfrac{BH}{BA}\)
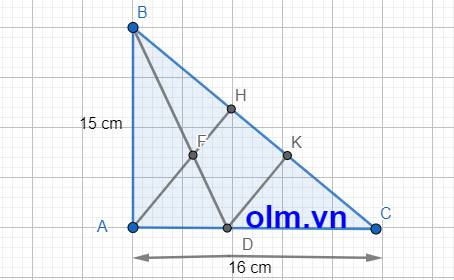
b, Theo pytago ta có: BC2 = AB2 + AC2 = 152+162 = 481 (cm2)
⇒ BC = \(\sqrt{481}\) cm
Kẻ đường cao DK vuông góc với BC cắt BC tại K
DA = DK ( vì mọi điểm trên tia phân giác thì cách đều hai cạnh còn lại)
Vì \(\Delta\)ABD và \(\Delta\)BCD có đường cao bằng nhau nên tỉ số diện tich hai tam giác bằng tỉ số hai cạnh đáy và bằng:
\(\dfrac{AB}{BC}\) = \(\dfrac{15}{\sqrt{481}}\)
Tương tự ta có tỉ số diện tích hai tam giác, tam giác ABD và tam giác BCD bằng:
\(\dfrac{AD}{DC}\) ⇒ \(\dfrac{AD}{DC}\) = \(\dfrac{15}{\sqrt{481}}\) ⇒ \(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\) = \(\dfrac{AD+DC}{15+\sqrt{481}}\) = \(\dfrac{16}{15+\sqrt{481}}\)
AD = \(\dfrac{16}{15+\sqrt{481}}\)\(\times\)15 = \(\dfrac{240}{15+\sqrt{481}}\) = \(\dfrac{15}{16}\)(\(\sqrt{481}\) - 15)
DC = \(\dfrac{16}{15+\sqrt{481}}\) \(\times\) \(\sqrt{481}\) = \(\dfrac{1}{16}\)(481 - 15\(\sqrt{481}\))

a: Xet ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
HB=6^2/10=3,6cm

a/ Xét tg vuông BAC và tg vuông BHA có
\(\widehat{ACB}=\widehat{BAH}\) (cùng phụ với \(\widehat{ABC}\) )
=> tg BAC đồng dạng với tg BHA (g.g.g)
b/ Xét tg vuông BAC có
\(BC=\sqrt{AB^2+AC^2}\) (Pitago) \(\Rightarrow BC=\sqrt{6^2+8^2}=10cm\)
\(AB^2=HB.BC\) (trong tg vuông bình phương 1 cạnh góc vuông bằng tích giữa hình chiếu cạnh góc vuông đó trên cạnh huyền với cạnh huyền)
\(\Rightarrow HB=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6cm\)
\(\Rightarrow HC=BC-HB=10-3,6=6,4cm\)
\(AH^2=HB.HC\) (Trong tg vuông bình phương đường cạo hạ từ đỉnh góc vuông bằng tích giữa hình chiếu của 2 cạnh góc vuông trên cạnh huyền)
\(\Rightarrow AH^2=3,6.6,4=23,04\Rightarrow AH=4,8cm\)
c/
Xét tg vuông HBM và tg vuông ABD có
\(\widehat{HBM}=\widehat{ABD}\left(gt\right)\) => tg HBM đồng dạng với tg ABD (g.g.g)
\(\Rightarrow\dfrac{HB}{AB}=\dfrac{HM}{AD}\Rightarrow\dfrac{AD}{AB}=\dfrac{HM}{HB}\) (1)
Xét tg vuông ABC có BD là phân giác \(\widehat{B}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}\) (T/c đường phân giác: Trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đợn thẳng tỷ lệ với hai cạnh kề hai đoạn thẳng đó) (2)
Xét tg ABH có BM là phân giác \(\widehat{B}\)
\(\Rightarrow\dfrac{HM}{HB}=\dfrac{AM}{AB}\) (T/c đường phân giác: Trong tg đường phân giác của 1 góc chia cạnh đối diện thành hai đợn thẳng tỷ lệ với hai cạnh kề hai đoạn thẳng đó) (3)
Từ (1) (2) (3) \(\Rightarrow\dfrac{AD}{AB}=\dfrac{CD}{BC}=\dfrac{HM}{HB}=\dfrac{AM}{AB}\)
\(\Rightarrow\dfrac{AD}{AB}.\dfrac{AM}{AB}=\dfrac{CD}{BC}.\dfrac{HM}{HB}\)
Mà \(HB.BC=AB^2\) (cmt)
\(\Rightarrow\dfrac{AD.AM}{AB^2}=\dfrac{HM.CD}{AB^2}\Rightarrow AM.AD=HM.CD\)
\(\Rightarrow AM.AD-HM.CD=0\)
a: Xét ΔBAH vuông tại H và ΔACH vuông tại H có
góc BAH=góc ACH
=>ΔHBA đồng dạg với ΔHAC
b: ΔHBA đồng dạng với ΔHAC
=>HB/HA=HA/HC
=>HA^2=HB*HC
c: BC=căn 6^2+8^2=10cm
Xét ΔBAH vuông tại H và ΔBCA vuông tại A có
góc B chung
=>ΔBAH đồng dạng với ΔBCA
=>S BAH/S BCA=(BA/BC)^2=9/25