Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=10cm
b: Xét ΔABE vuông tạiA và ΔDBE vuông tại D có
BE chung
góc ABE=góc DBE
=>ΔABE=ΔDBE
c: BA=BD
EA=ED
=>BE là trung trực của AD
d: góc HAD+góc BDA=90 độ
góc CAD+góc BAD=90 độ
mà góc BAD=góc BDA
nên góc HAD=góc CAD
=>AD là phân giác của góc HAC

Bài 1:
a, Xét tg ABD và tg EBD, có:
góc A= góc E(90o)
BD chung
góc ABD= góc DBE(tia phân giác)
=>tg ABD= tg EBD.
b, Ta có: tg ABD= tg DBE(cm câu a)
=>AB=BE(2 cạnh tương ứng)
=>tg ABE cân tại B.
Mà tg cân ABE có góc B=60o, nên tg ABE là tg đều.
c, Ta có: góc A+ góc B+góc C=180o(ĐL tổng 3 góc của tg)
=>góc B=180o-(góc A+ góc C)=180o-(90o+60o)=30o
Vì tg ABE là tg đều, nên góc A=60o.
Ta có: góc A=góc BAE+ góc AEC.
=>90o=60o+ góc AEC=30o.
=> góc AEC= góc C(=30o)
=>tg AEC cân tại E.
=>AE=EC.
Mà AE=5cm(tg đều), nên EC=5cm.
Vậy, độ dài cạnh BC là:
BE+EC=5+5=10.
=>BC= 10cm.

a) Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)(BD là tia phân giác của \(\widehat{ABE}\))
Do đó: ΔABD=ΔEBD(cạnh huyền-góc nhọn)

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
BA=BE
=>ΔBAD=ΔBED
b: ΔBAD=ΔBED
=>góc ABD=góc EBD
=>BD là phân giác của góc ABE
c: Xét ΔBEM vuông tại E và ΔBAC vuôg tại A có
BE=BA
góc EBM chung
=>ΔBEM=ΔBAC
=>BM=BC

a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>DA=DE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
c: BC=căn 3^2+4^2=5cm
d: BF=BC
DF=DC
=>BD là trung trực của CF


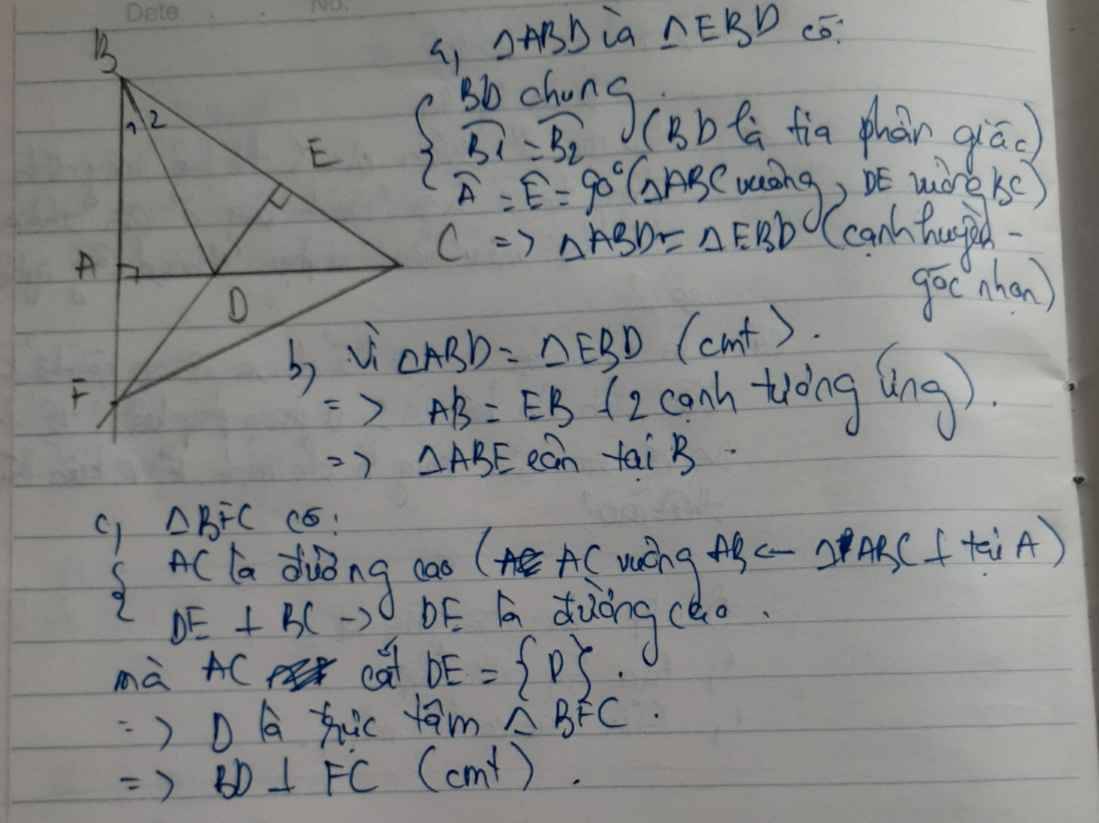
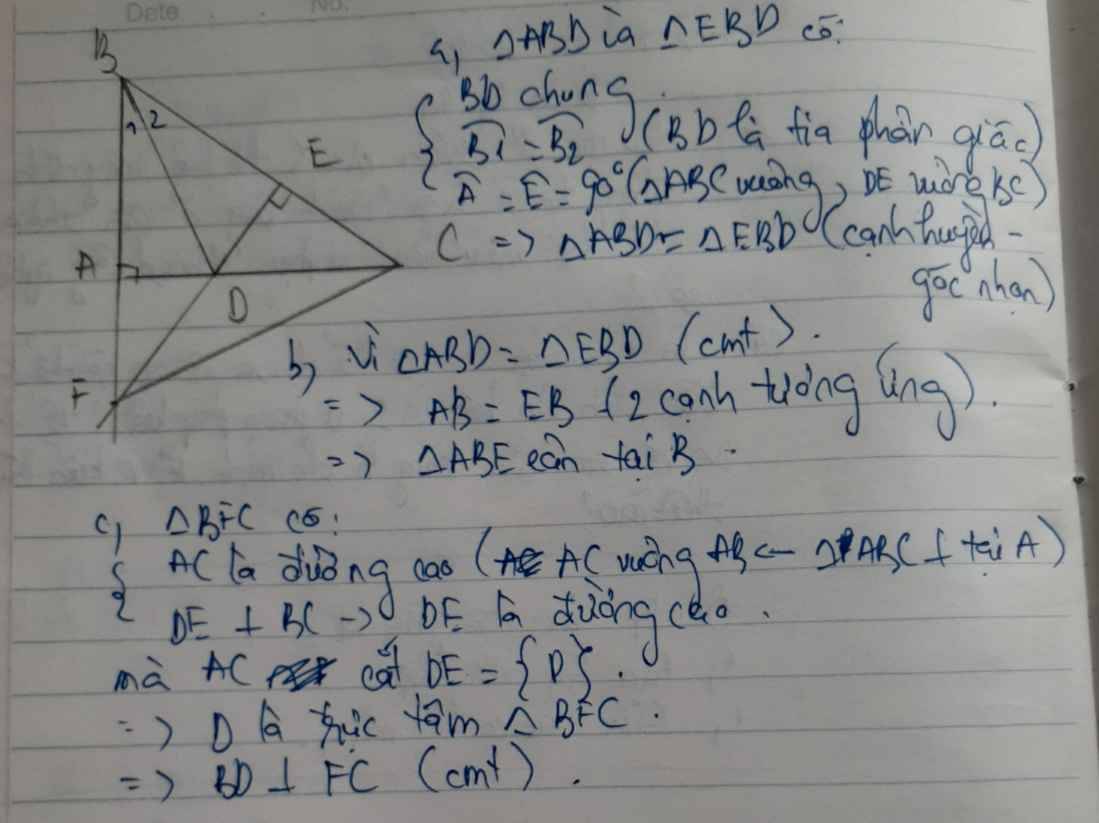

a) Xét tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\)
Thay số : \(AB^2=5^2-4^2=9\Rightarrow AB=3cm\)
b) Xét tam giác ABE và tam giác DBE có
\(\widehat{ABE}=\widehat{DBE}\left(gt\right)\)
\(\widehat{BAE}=\widehat{BDE}=90^o\)
BE chung
=> tam giác ABE = tam giác DBE (ch-gn)
c) Xét tam giác BMC có 2 đường cao CA và MD cắt nhau tại E
=> BE là đường cao thứ 3 của tam giác BMC
mà BE là phân giác của góc \(\widehat{ABC}\) hay \(\widehat{MBC}\)
=> tam giác BMC cân tại B (ĐPCM)
Câu C còn cách giả khác như sau
tam giác ABE = tam giác DBE (cmt)
=> AE = DE
Tam giác AME và DEC có
\(\widehat{MAE}=\widehat{CDE}=90^o\)
AE = DE
\(\widehat{AEM}=\widehat{DEC}\) (đối đỉnh)
=> tam giác AEM = tam giác DEC (g.c.g)
=> AM = DC
Có BA = BD (tam giác AEB = tam giác DEB)
AM = DC
=> BA + AM = BD + DC => BM = BC => tam giác BMC cân
À mà mình lớp 10 nha