Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì \(\Delta ABC\) vuông tại A (giả thiết).
\(\Rightarrow AB^2+AC^2=BC^2\)(định lí Py-ta-go).
\(\Rightarrow6^2+8^2=BC^2\)(thay số).
\(\Rightarrow BC^2=36+64=100\)
\(\Rightarrow BC=10\left(cm\right)\)(vì \(BC>0\)).
Xét \(\Delta ABC\)có phân giác BD (giả thiết).
\(\Rightarrow\frac{AD}{CD}=\frac{AB}{CB}\)(tính chất).
\(\Rightarrow\frac{AD}{CD+AD}=\frac{AB}{CB+AB}\)(tính chất của tỉ lệ thức).
\(\Rightarrow\frac{AD}{AC}=\frac{AB}{BC+BA}\)
\(\Rightarrow\frac{AD}{8}=\frac{6}{6+10}=\frac{6}{16}=\frac{3}{8}\)(thay số).
\(\Rightarrow AD=\frac{3}{8}.8=3\left(cm\right)\)
Do đó \(CD=AC-AD=8-3=5\left(cm\right)\)
Vậy \(AD=3\left(cm\right),CD=5\left(cm\right)\)

\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BD là phân giác
=>DA/AB=DC/BC
=>DA/3=DC/5=8/8=1
=>DA=3cm; DC=5cm

A B C 6 8 10 H D D
a, dễ mà dài, bạn tự làm nhé
b, Vì AD là đường pg của tam giác ABC nên
\(\frac{AC}{AB}=\frac{CD}{BD}\)( tính chất )
mà \(BD=BC-CD=10-CD\)(*)
\(\Rightarrow\frac{8}{6}=\frac{CD}{10-CD}\Rightarrow CD=\frac{40}{7}\)cm
Theo (*) suy ra : \(BD=10-\frac{40}{7}=\frac{30}{7}\)cm

a: BC=căn 6^2+8^2=10cm
AD là phân giác
=>DB/AB=DC/AC
=>DB/3=DC/4=(DB+DC)/(3+4)=10/7
=>DB=30/7cm; DC=40/7cm
b: Xét ΔAHB vuông tại H và ΔCHA vuông tại H có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: AH=8*6/10=4,8cm
HB=6^2/10=3,6cm
CH=10-3,6=6,4cm
S AHB=1/2*4,8*3,6=8,64cm2
S AHC=1/2*4,8*6,4=15,36cm2

a) Gọi x(cm) là độ dài cạnh DB
Áp dụng định lý Pi-ta-go vào tam giác ABC vuông tại A, ta có:
BC2= AB2 + AC2= 82 + 62= 100
=>BC=\(\sqrt{100}\)=10(cm)
Xét tam giác ABC, ta có:
AD là tia phân giác góc A
=> \(\frac{DB}{AB}=\frac{DC}{AC}hay\frac{x}{8}=\frac{10-x}{6}\)
=> 6x = 8(10-x)
<=>6x=80-8x
<=>6x + 8x=80
<=> 14x=80
<=> x= 5,72(cm)
Vậy DB= 5,72 cm
DC= 10 - 5,72= 4,28 (cm)
a. tam giác ABC có góc A = 90 độ nên
BC^2=AB^2+AC^2
=8^2+6^2=100
=>BC =10
áp dụng tính chất dãy tỉ số bằng nhau ta có :
BD/AB=DC/AC =BD+DC/AB+AC=10/14=5/7
=>BD/AB=5/7=>BD=8*5:7=40/7
=>DC/Ac=5/7=>DC=6*5/7=30/7
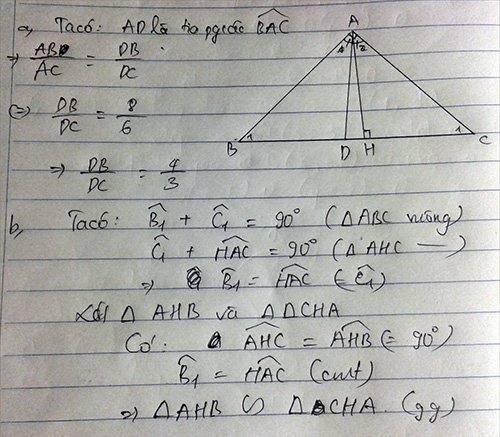
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: \(BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=4.8\left(cm\right)\)
a) Xét ∆ABC và ∆HBA, ta có:
<A=<H=90°
<B chung
⟹∆ABC∼∆HBA(g.g)
b) Áp dụng định lý py-ta-go vào ∆ABC(<A=90°(gt)) , ta có:
BC2 =AB2+AC2
=82+62=64+36=100
⟹BC=√100=10cm
Ta có: AC/HA=BC/AB ( Vì ∆ABC∼∆HBA(CM ở a))
⟹6/HA=10/8⟹HA=6*8/10=4,8cm