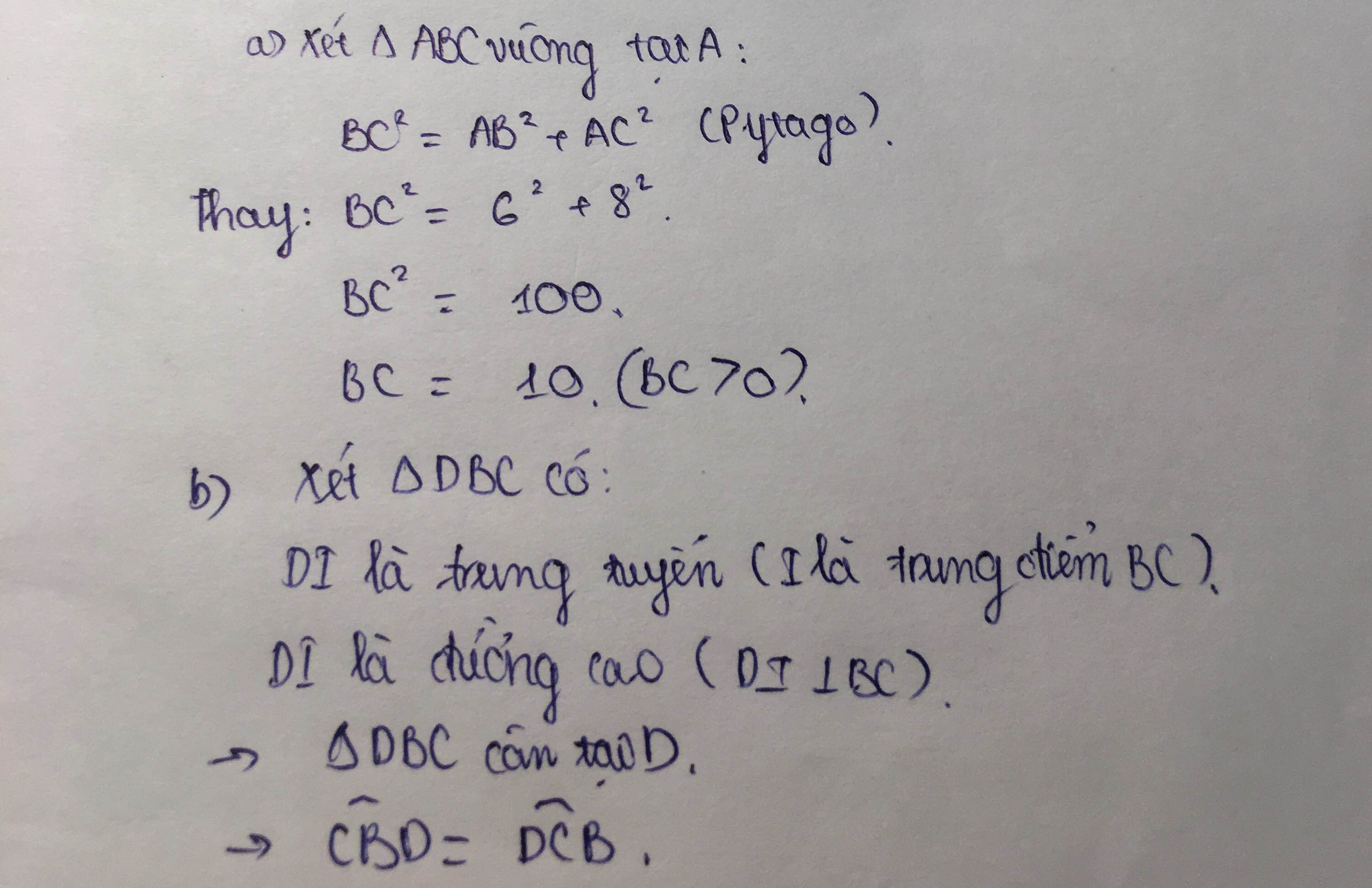K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

25 tháng 4 2018
a) Áp dụng đ/lý pytago vào Δ vuông ABC, có:
AC^2 + AB ^2 = BC ^2
8^2 + 6^2 = BC ^2
BC ^2 = 64 + 36
BC ^2 = 100
=>BC = 10 cm

3 tháng 7 2022
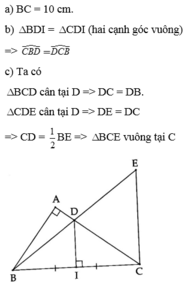
a:BC=10cm
b: Ta có: D nằm trên đường trung trực của BC
nên DB=DC
=>ΔDBC cân tại D
=>góc DBC=góc DCB
c: Xét ΔBCE có
CD là đường trung tuyến
CD=BE/2
Do đó:ΔBCE vuông tại C

PD
5 tháng 1 2021
giúp mình với nhé mai mình thi cuối học kì I môn toán rồi. Chúc các bạn có một kì thi tốt đẹp.
5 tháng 1 2021
đề bài sai à
câu a tam giác vuông tại A mà góc B = 90o suy ra góc C = 0o à

10 tháng 7 2017
a) xét tam giác ABD và tam giác ACD có
AB=AC,AD là cạnh chung góc BAD= góc DAC
vậy tam giác ABD=tam giác ACD(C.g.c)
Suy ra gócADB=gócADC=1/2BDC=1/2*180=90
Hay AD vuông góc với BC