
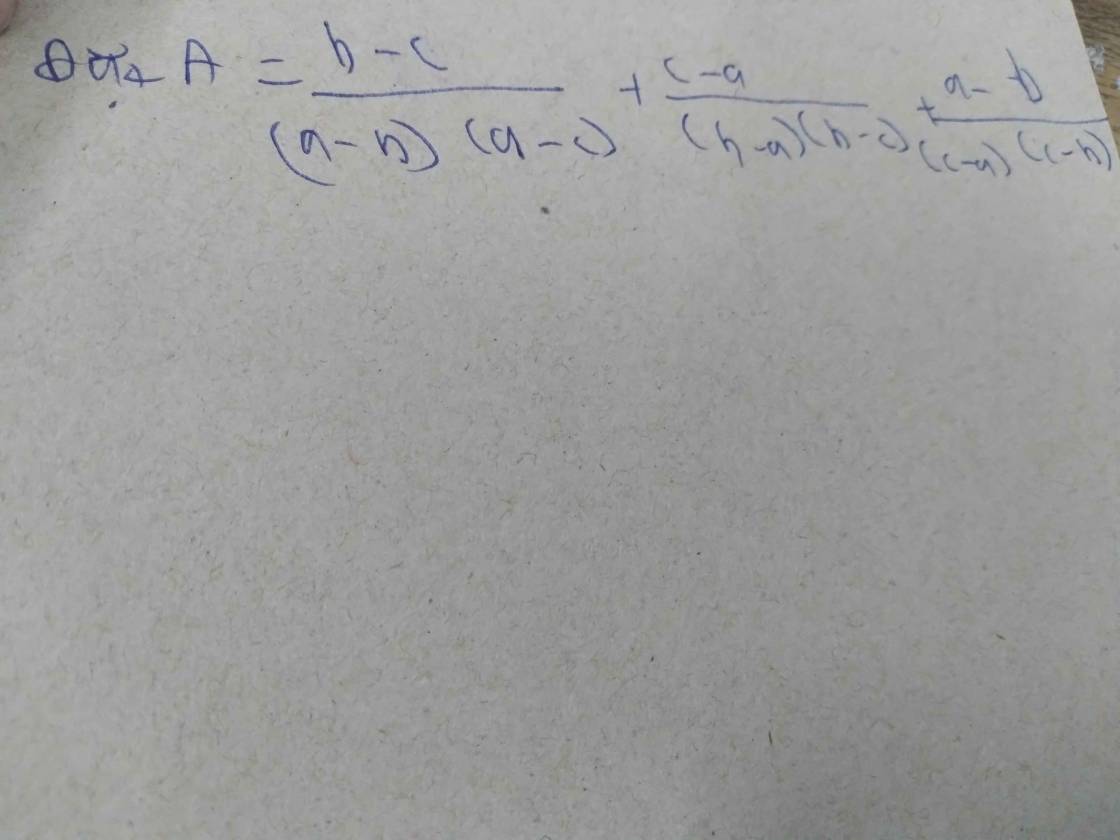
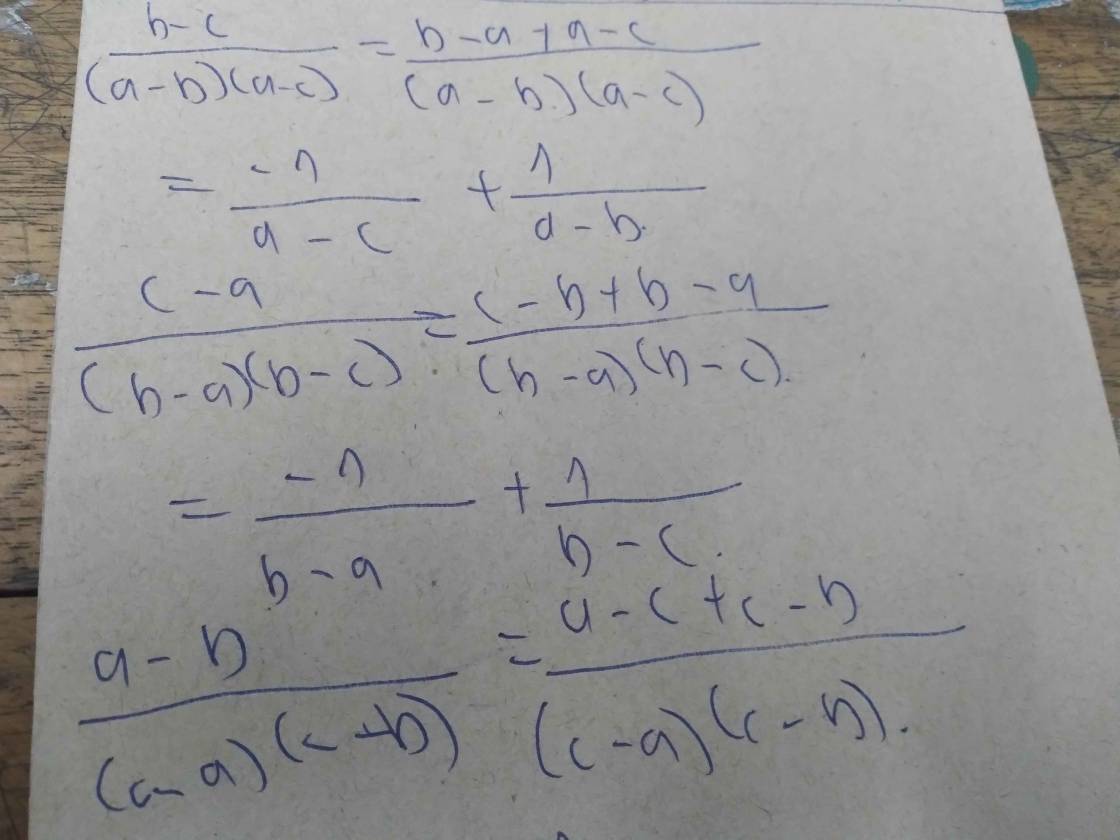
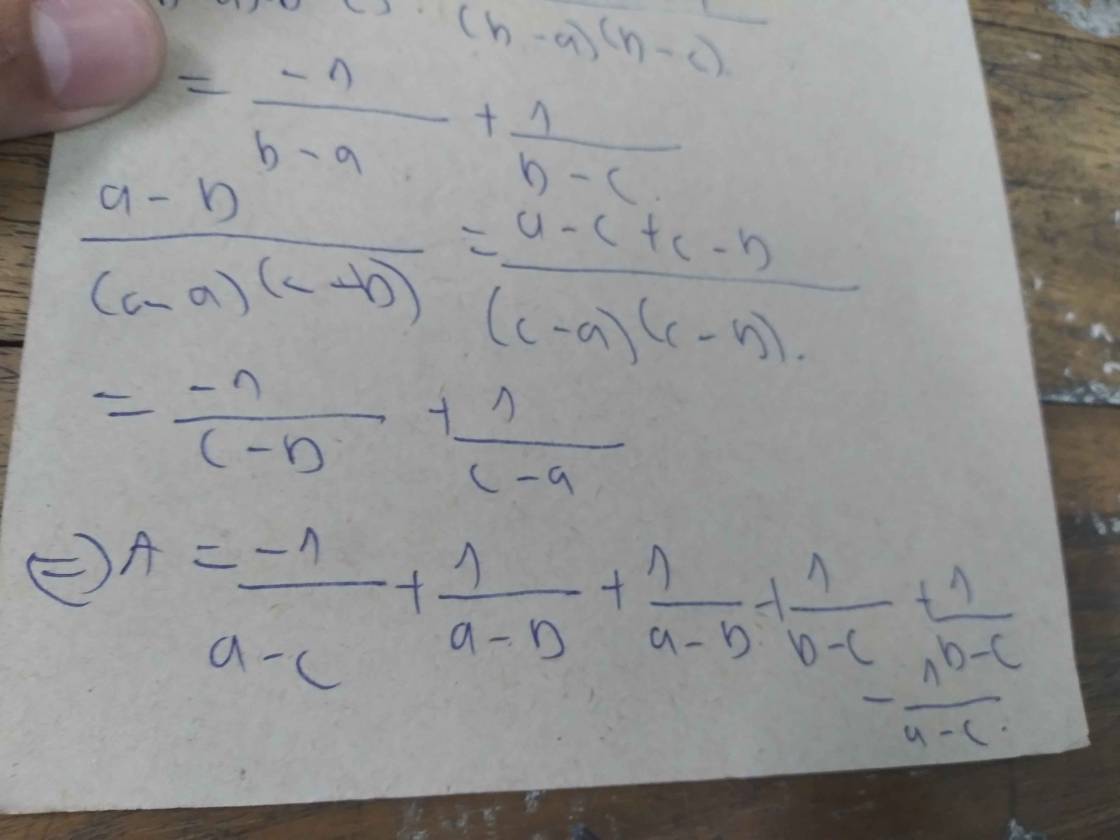
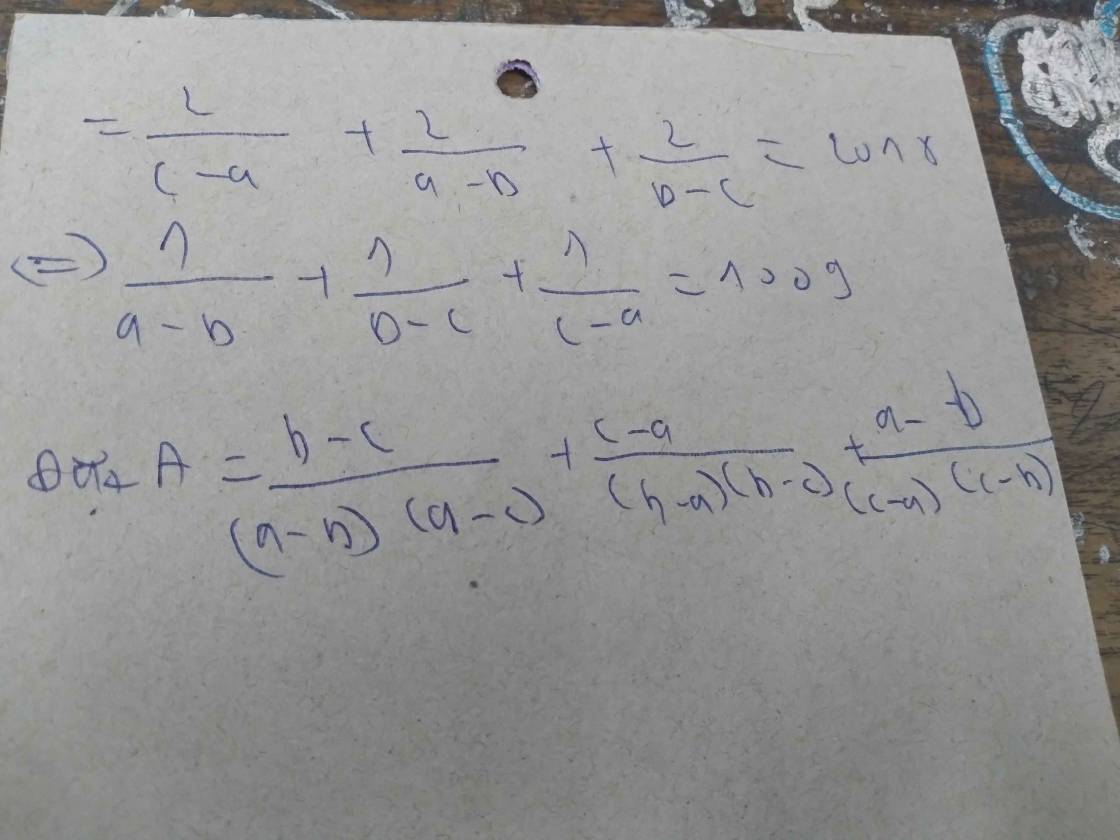
(b-c)/(a-b)(a-c)+(c-a)/(b-a)(b-c)...">
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

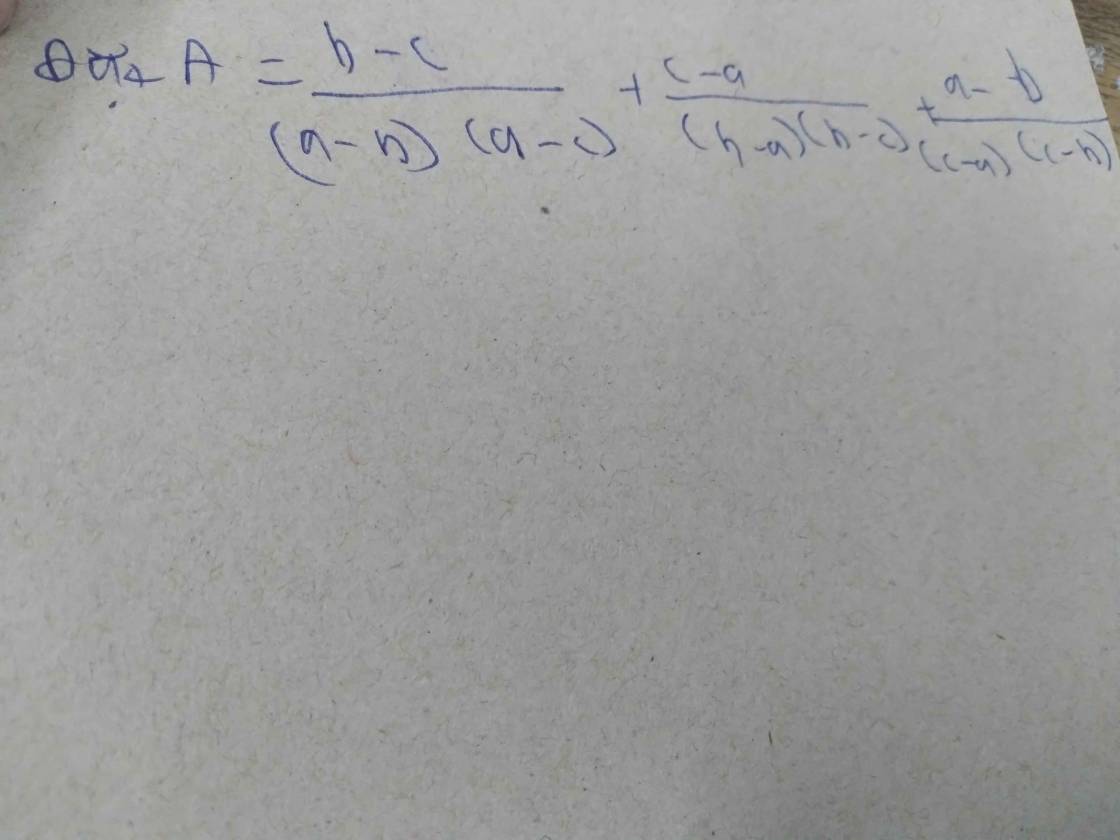
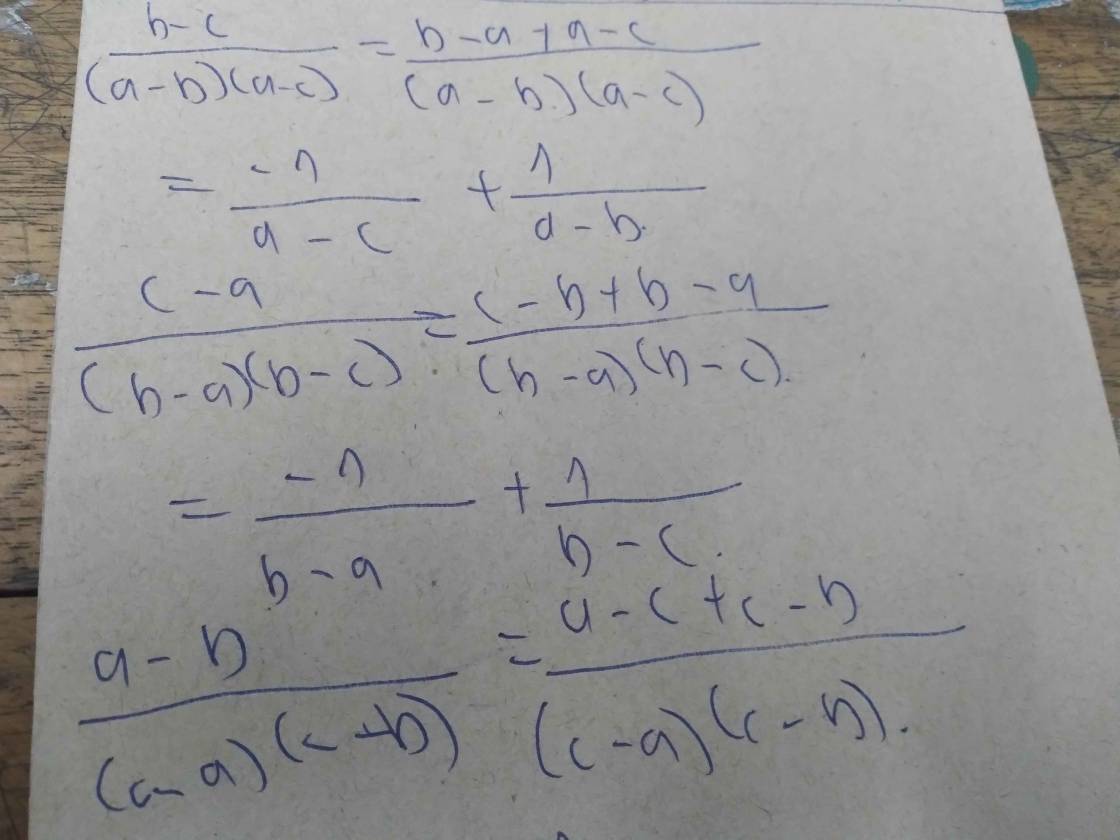
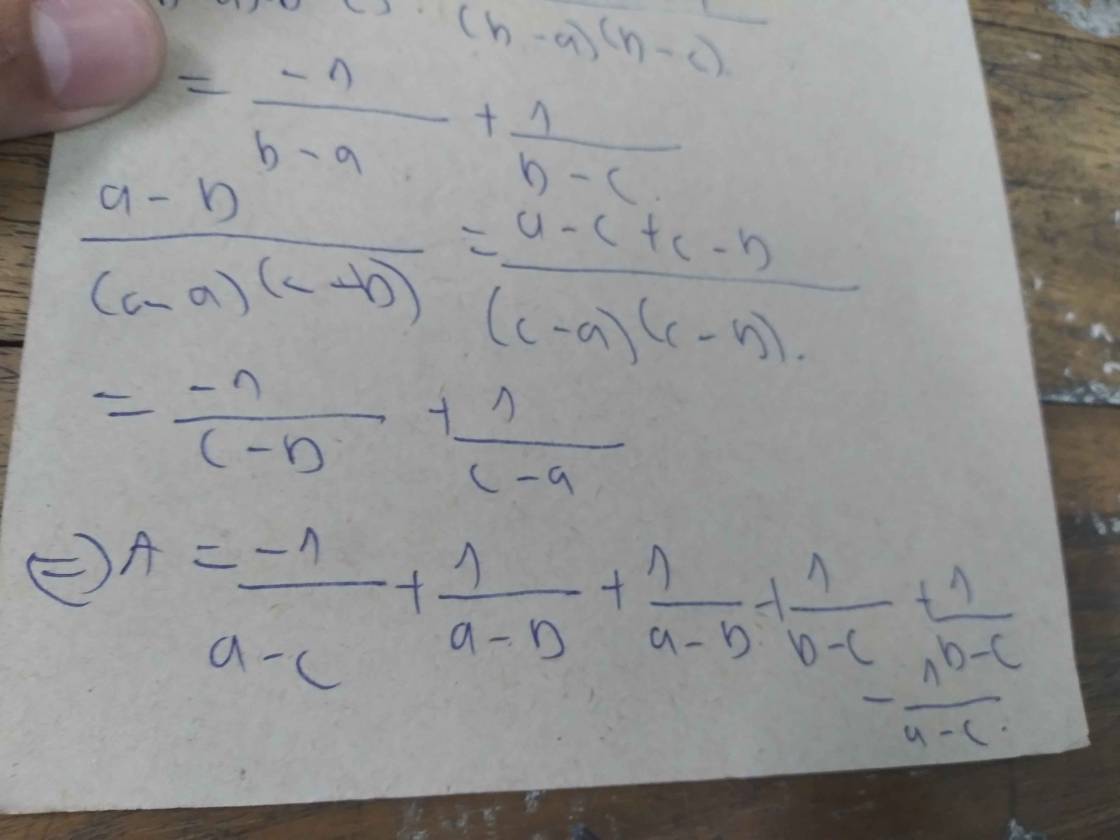
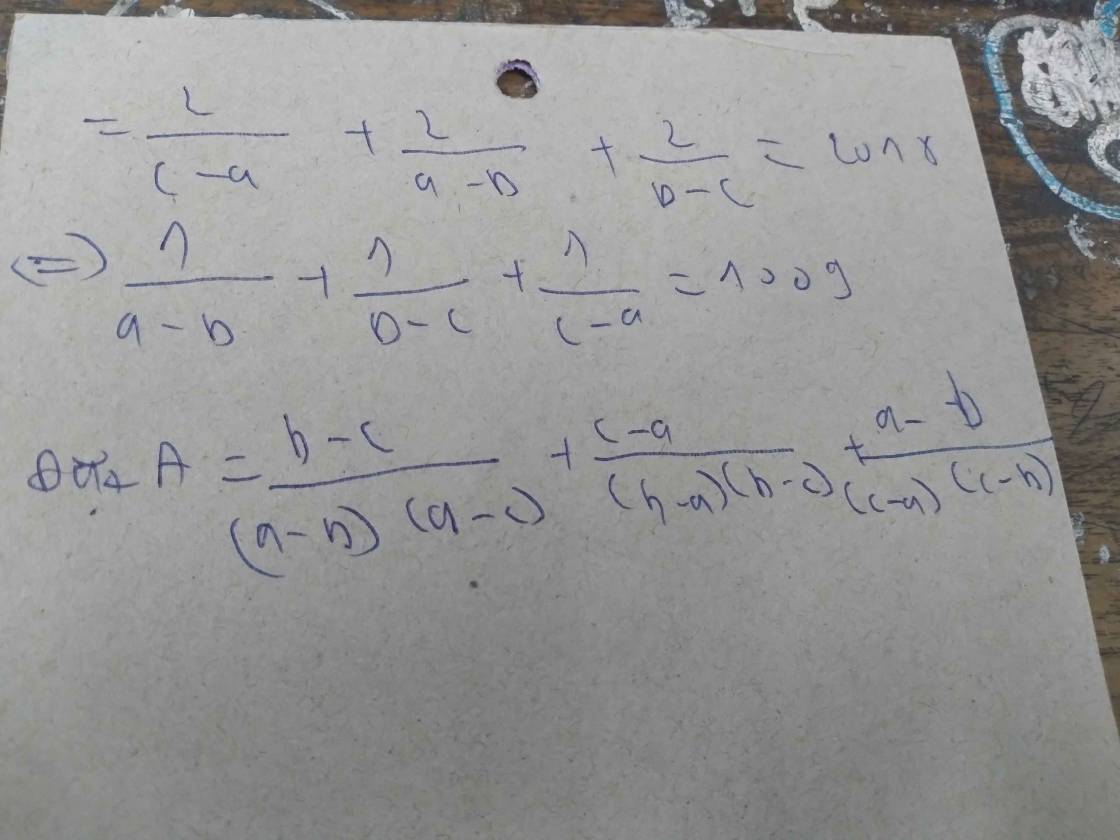

xét a +b+c = 0 => a+b=-c; c+a=-b;b+c=-a
thay vào B ta sẽ đc B = -1
XÉT a+b+c khác 0
áp dụng tính chất của dãy tỉ số bằng nhau
=> a+b=2c;b+c=2a;a+c=2b
=>S = 8
Theo t/c dãy tỉ số=nhau:
\(\frac{a+b-c}{c}=\frac{b+c-a}{a}=\frac{c+a-b}{b}=\frac{a+b-c+b+c-a+c+a-b}{c+a+b}=\frac{a+b+c}{c+a+b}=1\)
=>a+b-c=c =>a+b=2c (1)
b+c-a=a=>b+c=2a (2)
c+a-b=b=>c+a=2b (3)
Thay (1);(2);(3) vào B ta có;
\(B=\left(1+\frac{b}{a}\right)\left(1+\frac{a}{c}\right)\left(1+\frac{c}{b}\right)=\frac{a+b}{a}.\frac{c+a}{c}.\frac{b+c}{b}=\frac{2c}{a}.\frac{2b}{c}.\frac{2a}{b}=\frac{2c.2b.2a}{a.c.b}=2.2.2=8\)
Vậy B=8

Ta có:
\(\frac{a+b-c}{c}=\frac{b+c-a}{a}=\frac{c+a-b}{b}\)
\(<=>\frac{a+b-c}{c}+2=\frac{b+c-a}{a}+2=\frac{c+a-b}{b}+2\)
\(<=>\frac{a+b-c+2c}{c}=\frac{b+c-a+2a}{a}=\frac{c+a-b+2b}{b}\)
\(<=>\frac{a+b+c}{c}=\frac{a+b+c}{a}=\frac{a+b+c}{b}\)
\(<=>\left(a+b+c\right)\times\frac{1}{c}=\left(a+b+c\right)\times\frac{1}{a}=\left(a+b+c\right)\times\frac{1}{b}\)
\(<=>\frac{1}{a}=\frac{1}{c}=\frac{1}{b}<=>a=c=b\)
Vậy:
\(A=\left(1+\frac{b}{a}\right)\left(1+\frac{a}{c}\right)\left(1+\frac{c}{b}\right)=\left(1+\frac{a}{a}\right)\left(1+\frac{c}{c}\right)\left(1+\frac{b}{b}\right)\)
\(A=\left(1+1\right)\left(1+1\right)\left(1+1\right)=2^3=8\)
Vậy A=8

\(\Leftrightarrow\frac{a+b}{c}+1=\frac{b+c}{a}+1=\frac{c+a}{b}\Leftrightarrow\frac{a+b+c}{c}=\frac{a+b+c}{a}=\frac{a+b+c}{b}\)
=> a= b =c
=> P = (1+1) ( 1+1)(1+1) = 2.2.2 =8

Ta có: (a+b-c)/c=(b+c-a)/a=(c+a-b)/b=(a+b-c+b+c... (a+b+c)=(a+b+c)/(a+b+c)=1
=>(a+b-c)/c=1 => a+b-c=c =>a+b=2c (1)
Tương tự: (b+c-a)/a=1 =>b+c=2a (2)
(c+a-b)/b=1 =>c+a=2b (3)
Thay (1), (2), (3) vào B, ta có:
B=(a+b)/a . (b+c)/b .(a+c)/c=2c/a.2a/b.2b/c=2.2.2=8.
(a+b-c)/c+2=(b+c-a)/a+2=(c+a-b)/b+2
<=> (a+b+c)/c=(b+c+a)/a=(c+a+b)/b
Nếu a+b+c=0 => (a+b)/a.(b+c)/b.(c+a)/c=((-c)(-a)(-b))/a...
Nếu a+b+c khác 0 =>a=b=c =>P=2.2.2=8 .
tích nha