Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Bạn tự vẽ hình nhé!
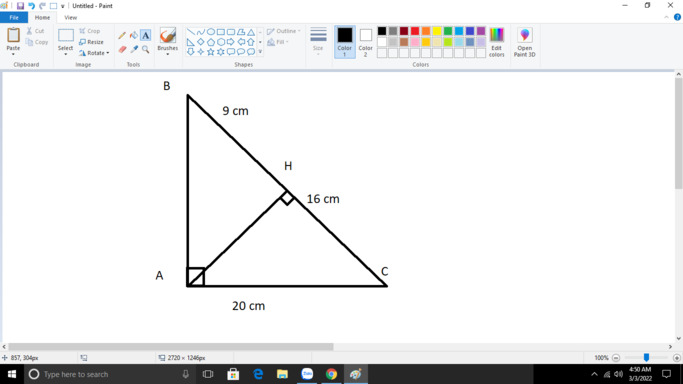
Áp dụng đ/lí Pi-ta-go trong tam giác ABC vuông tại A có:
BC2 = AB2 + AC2
hay BC2 = 202 + 152
=> BC2 = 625 = 252
=> BC = 25 (cm)
Áp dụng đ/lí Pi-ta-go trong tam giác AHB vuông tại H có:
AB2 = AH2 + HB2
=> BH2 = AB2 - AH2
=> BH2 = 202 - 122
=> BH2 = 256 = 162
=> BH = 16 (cm)
Mà H thuộc BC nên H nằm giữa BC
=> BH + HC = BC
=> 16 + HC = 25
=> HC = 25 - 16
=> HC = 9 (cm)
Vậy BC = 25 cm; BH = 16 cm; CH = 9 cm.

△ABC vuông tại A có \(BC^2=AB^2+AC^2\\ \Rightarrow BC=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(\Rightarrow CH=BC-BH=25-9=16\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=15^2+20^2=625\)
hay BC=25(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên CH=BC-BH=25-9=16(cm)
Vậy: CH=16cm

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=20^2-12^2=256\)
hay AC=16(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7.2\left(cm\right)\\CH=\dfrac{AC^2}{BC}=\dfrac{16^2}{20}=12.8\left(cm\right)\end{matrix}\right.\)
Áp dụng định lí Pytago vào ΔABH vuông tại H, ta được:
\(AB^2=AH^2+HB^2\)
\(\Leftrightarrow AH^2=AB^2-HB^2=12^2-7.2^2=92.16\)
hay AH=9,6(cm)
Vậy: AC=16cm; BH=7,2cm; CH=12,8cm; AH=9,6cm

Tam giác AHB vuông tại H => AH2 + BH2 = AB2 ( định lí Py-ta-go)
=> 122 + BH2 = 152
=> BH = 152 - 122 = 81
=> BH = 9 ( vì BH > 0) (1)
Tam giác AHC vuông tại H => AH2 + HC2 = AC2 ( định lí Py-ta-go)
=> 122 + HC = 202
=> HC = 202 - 122 = 256
=> HC = 16 ( vì HC > 0) (2)
Từ (1) và (2) BH + HC = 9 + 16
=> BC = 25
Dễ thấy, 152 + 202 = 252
=> AB2 + AC2 = BC2
=> Tam giác ABC vuông tại A ( định lí Py-ta-go đảo) hay BAC = 90o (đpcm)

Ta có: BC = HB+HC = 9+16=25cm
Áp dụng định lý pitago vào tam giác vuông ABC, có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{25^2-20^2}=\sqrt{225}=15cm\)
Áp dụng định lý pitago vào tam giác vuông ABH, có:
\(AB^2=AH^2+BH^2\)
\(\Rightarrow AH=\sqrt{AB^2-BH^2}=\sqrt{15^2-9^2}=\sqrt{144}=12cm\)
\(BC=BH+HC\)
\(\Rightarrow BC=9cm+16cm=25\left(cm\right)\)
\(\text{Xét }\Delta ABC\text{ vuông tại }A\text{ có:}\)
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB^2=BC^2-AC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AB^2=25^2-20^2=625-400=225\left(cm\right)\)
\(\Rightarrow AB=\sqrt{225}=15\left(cm\right)\)
\(\text{Xét }\Delta AHC\text{ vuông tại }H\text{ có:}\)
\(AC^2=AH^2+HC^2\)
\(\Rightarrow AH^2-AC^2-HC^2\text{(định lí Py ta go đảo)}\)
\(\Rightarrow AH^2=20^2-16^2=400-256=144\left(cm\right)\)
\(\Rightarrow AH=\sqrt{144}=12\left(cm\right)\)

Mình làm tóm tắt thôi nhé! Cậu tự giải sẽ nhớ lâu hơn!
Câu a) định lý Pytago đảo
b)Áp dụng định lí Pytago vào tam giác ABH

Xét tam giác ABC cân tại A: M là trung điểm của BC(gt)
=> AM là trung tuyến
Xét tam giác ABC cân tại A: AM là trung tuyến (cmt)
=> AM là đường cao (TC các đường trong tam giác cân)
Xét tam giác EBC: EM là trung tuyến (AM là trung tuyến, E thuộc AM)
EM là đường cao (AM là đường cao, E thuộc AM)
=> Tam giác EBC cân tại E
M là trung điểm của BC (gt) => BM = \(\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Xét tam giác AMB vuông tại M (AM \(\perp BM\))
AB2 = AM2 + BM2 (định lý Py ta go)
Thay số: AB2 = 82 + 62
<=> AB2 = 100
<=> AB = 10 (cm)
Vậy AB = 10 (cm)
Bài 1:
Xét ∆ABC vuông tại A, AH \(\perp\) BC:
Ta có: AH2 = BH . HC (hệ thức lượng)
<=> 122 = 9 . HC
<=> HC = \(\dfrac{12^2}{9^{ }}=\dfrac{144}{9}=16\left(cm\right)\)
Vậy HC = 16 (cm)
Ta có: BC = BH + HC = 9 + 16 = 25 (cm)
Xét ∆ABC vuông tại A, AH \(\perp\) BC:
Ta có: AB2 = BH . BC (hệ thức lượng)
<=> AB2 = 9 . 25
<=> AB2 = 225
<=> AB = 15 (cm)
Vậy AB = 15 (cm)
Ta có:
+)\(AH\perp BC\left(gt\right)\)
\(\Rightarrow\widehat{H_1}=\widehat{H_2}=90^0\)
Xét \(\Delta AHC\) có \(\widehat{H_1}=90^0\left(cmt\right)\Rightarrow\Delta AHC\) vuông tại \(H\)
\(\Rightarrow AC^2=AH^2+HC^2\)(Định lý Py-ta-go)
\(\Leftrightarrow15^2=20^2+HC^2\)
\(\Leftrightarrow225=400+HC^2\)
.....
Mà như thế thì HC âm nên ko thỏa mãn nên tớ nghĩ bài này sai sai òi