Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
BM là đường cao
CN là đường cao
BM cắt CN tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC
b: Xét tứ giác AMHN có \(\widehat{AMH}+\widehat{ANH}=180^0\)
nên AMHN là tứ giác nội tiếp
c: Xét tứ giác BCMN có \(\widehat{BNC}=\widehat{BMC}=90^0\)
nên BCMN là tứ giác nội tiếp

a, Ta có: $HM⊥AB;HN⊥AC$
$⇒\widehat{HMA}=\widehat{HNA}=90^o$
$⇒\widehat{HMA}+\widehat{HNA}=180^o$
$⇒$ Tứ giác $AMHN$ nội tiếp (Tổng 2 góc đối $=180^o$)
b, Xét tam giác $AHB$ vuông tại $H$
Đường cao $HM$ (do $HM⊥AB$)
Nên $AH^2=AM.AB(1)$
Xét tam giác $AHC$ vuông tại $H$
Đường cao $HN$ (do $HN⊥AB$)
Nên $AH^2=AN.AC(2)$
Từ $(1)(2)⇒AM.AB=AN.AC$
$⇒\dfrac{AM}{AC}=\dfrac{AN}{AB}$
Xét tam giác $AMN$ và tam giác $ACB$ có:
$\dfrac{AM}{AC}=\dfrac{AN}{AB}$
$\widehat{A}$ chung
$⇒$ tam giác $AMN$ $\backsim$ tam giác $ACB(c.g.c)$
(đpcm)
c, tam giác $AMN$ $\backsim$ tam giác $ACB$
$⇒\widehat{ANM}=\widehat{ABC}$
Xét $(O)$ có: $\widehat{ABC}=\widehat{AEC}$ (các góc nội tiếp cùng chắn cung $AC$)
Nên $\widehat{ANM}=\widehat{AEC}$
Hay $\widehat{ANI}=\widehat{IEC}$
$⇒$ Tứ giác $CEIN$ nội tiếp (góc ngoài tại 1 đỉnh = góc trong đỉnh đối diện)
c, Ta có: $\widehat{ANM}=\widehat{ABC}$
Mà $\widehat{ABC}+\widehat{AKC}=180^o$
do tứ giác $ABCK$ nội tiếp $(O)$
Nên $\widehat{ANM}+\widehat{AKC}=180^o$
Mà $\widehat{ANM}+\widehat{ANK}=180^o$
Nên $\widehat{AKC}=\widehat{ANK}$
Xét tam giác $AKC$ và tam giác $ANK$ có:
$\widehat{AKC}=\widehat{ANK}$
$\widehat{A}$ chung
nên tam giác $AKC$ $\backsim$ tam giác $ANK(g.g)$
$⇒\dfrac{AK}{AN}=\dfrac{AC}{AK}$
$⇒AK^2=AN.AC$
mà $AH^2=AN.AC(cmt)$
$⇒AK^2=AH^2$
hay $AK=AH$
suy ra tam giác $AHK$ cân tại $A$

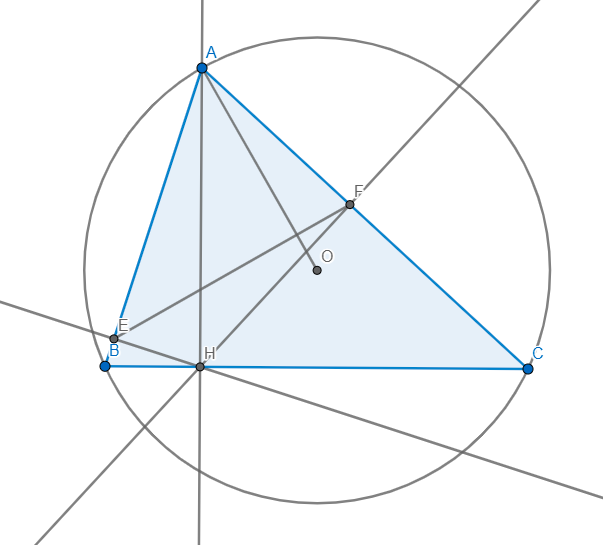
a) Ta có: \(\angle AEH+\angle AFH=90+90=180\Rightarrow AEHF\) nội tiếp
b) AEHF nội tiếp \(\Rightarrow\angle EFA=\angle EHA=90-\angle BHE=\angle ABC\)
c) Ta có: \(\angle OAC=\dfrac{180-\angle AOC}{2}=90-\dfrac{1}{2}\angle AOC=90-\angle ABC\)
\(\Rightarrow\angle OAC+\angle ABC=90\Rightarrow\angle OAC+\angle AFE=90\Rightarrow OA\bot EF\)