Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dễ thấy \(0< a,b,c< \frac{3}{2}\)
Thật vậy nếu g/s ngược lại tồn tại 1 số >= 3/2 và g/s đó là a
\(\Rightarrow a\ge b+c\) mâu thuẫn với BĐT tam giác nên ta có điều như trên
Ta có: \(\left(\frac{3}{2}-a\right)+\left(\frac{3}{2}-b\right)+\left(\frac{3}{2}-c\right)\ge3\sqrt[3]{\left(\frac{3}{2}-a\right)\left(\frac{3}{2}-b\right)\left(\frac{3}{2}-c\right)}\)
\(\Leftrightarrow\frac{9}{2}-\left(a+b+c\right)\ge3\sqrt[3]{\left(\frac{3}{2}-a\right)\left(\frac{3}{2}-b\right)\left(\frac{3}{2}-c\right)}\)
\(\Leftrightarrow\frac{1}{2}\ge\sqrt[3]{\left(\frac{3}{2}-a\right)\left(\frac{3}{2}-b\right)\left(\frac{3}{2}-c\right)}\)
\(\Leftrightarrow\frac{1}{8}\ge\left(\frac{3}{2}-a\right)\left(\frac{3}{2}-b\right)\left(\frac{3}{2}-c\right)\)
\(\Leftrightarrow\frac{1}{8}\ge\left(\frac{9}{4}-\frac{3}{2}a-\frac{3}{2}b+ab\right)\left(\frac{3}{2}-c\right)\)
\(\Leftrightarrow\frac{1}{8}\ge\frac{27}{8}-\frac{9}{4}\left(a+b+c\right)+\frac{3}{2}\left(ab+bc+ca\right)-abc\)
\(\Leftrightarrow\frac{1}{8}\ge\frac{27}{8}-\frac{27}{4}+\frac{3}{2}\left(ab+bc+ca\right)-abc\)
\(\Leftrightarrow\frac{3}{2}\left(ab+bc+ca\right)-abc\le\frac{7}{2}\)
\(\Leftrightarrow6\left(ab+bc+ca\right)-4abc\le14\)
\(\Leftrightarrow4abc\ge6\left(ab+bc+ca\right)-14\)
\(\Leftrightarrow3a^2+3b^2+3c^2+4abc\ge3\left(a+b+c\right)^2-14\)
\(\Leftrightarrow3a^2+3b^2+3c^2+4abc\ge13\)
Dấu "=" xảy ra khi: a = b = c = 1

chúa muốn hỏi , đề sai hay đúng ở chỗ " 3c^3+2ca+3c^2 ý :))

Ta có:
A = \(\frac{a}{2b+3c}+\frac{b}{2c+3a}+\frac{c}{3b+2a}=\frac{a^2}{2ab+3ac}+\frac{b^2}{2bc+3ab}+\frac{c^2}{3bc+2ac}\)
A \(\ge\frac{\left(a+b+c\right)^2}{2ab+3ac+2bc+3ab+3bc+2ac}\)(bđt svacxo \(\frac{x_1^2}{y_1}+\frac{x_2^2}{y_2}+\frac{x_3^2}{y_3}\ge\frac{\left(x_1+x_2+x_3\right)^2}{y_1+y_2+y_3}\))
A \(\ge\frac{\left(a+b+c\right)^2}{5\left(ab+bc+ac\right)}\ge\frac{\left(a+b+c\right)^2}{\frac{5\left(a+b+c\right)^2}{3}}\) (bđt \(xy+yz+xz\le\frac{\left(x+y+z\right)^2}{3}\)(*)
CM bđt * <=> \(3xy+3yz+3xz\le x^2+y^2+z^2+2xz+2xy+2yz\)
<=> \(\left(x-y\right)^2+\left(x-z\right)^2+\left(y-z\right)^2\ge0\) (luôn đúng)
<=> A \(\ge\frac{3}{5}\) --> ĐPCM

giả sử a+b+c=k>0; đặt a=kx; b=ky; c=kz => x;y;z>0 và x+y+z=1
khi đó P=k\(\left[\frac{k\left(3x-y\right)}{k^2\left(x^2+xy\right)}+\frac{k\left(3y-z\right)}{k^2\left(y^2+yz\right)}+\frac{k\left(3z-x\right)}{k^2\left(z^2+zx\right)}\right]=\frac{3x-y}{x^2+xy}+\frac{3y-z}{x^2+xy}+\frac{3z-x}{z^2+zx}\)
\(=\frac{4x-\left(x+y\right)}{x\left(x+y\right)}+\frac{4y-\left(y+z\right)}{y\left(y+z\right)}+\frac{4z-\left(z+x\right)}{z\left(z+x\right)}=\frac{4}{x+y}-\frac{1}{x}+\frac{4}{y+z}-\frac{1}{y}+\frac{4}{z+x}-\frac{1}{z}\)
\(=\frac{4}{1-z}-\frac{1}{x}+\frac{1}{1-x}+\frac{1}{y}+\frac{1}{1-y}+\frac{1}{z}=\frac{5x-1}{x-x^2}+\frac{5y-1}{y-y^2}+\frac{5z-1}{z-z^2}\)
do a,b,c là 3 cạnh của 1 tam giác => b+c>a =>y+z>x => 1-x>x
=> x<1/2 tức là a\(\in\left(0;\frac{1}{2}\right)\)tương tự ta cũng có: \(y;z\in\left(0;\frac{1}{2}\right)\)
ta sẽ chứng minh \(\frac{5t-1}{t-t^2}\le18t-3\)(*) đúng với mọi \(\in\left(0;\frac{1}{2}\right)\)
thật vậy (*) \(\Leftrightarrow\frac{5t-1}{t-t^2}-18t+3\le0\Leftrightarrow\frac{18t-21t^2+8t-1}{t-t^2}\le0\Leftrightarrow\frac{\left(2t-1\right)\left(3t-1\right)^2}{t\left(t-1\right)}\le0\)(**)
(**) hiển nhiên đúng với mọi \(t\in\left(0;\frac{1}{2}\right)\)do đó (*) đúng với mọi \(t\in\left(0;\frac{1}{2}\right)\)
áp dụng (*) ta được \(P\le18x-3+18y-3=18\left(x+y+z\right)-9=9\)
dấu "=" xảy ra <=> x=y=z=1/3 <=> a=b=c
@Hai Ngox: Sao phải giả sử a + b + c = k > 0 vậy bạn? Vì a,b,c là độ dài 3 cạnh của tam giác thì đó là hiển nhiên.
Ngoài ra:
Nó tương đương với \(\Sigma c^2\left(b+c\right)\left(a+c\right)\left(a-b\right)^2\ge0\) (1)
Hoặc \(\Sigma a^4\left(b-c\right)^2+\frac{1}{3}\left(ab+bc+ca\right)\Sigma\left(2ab-bc-ca\right)^2\ge0\) (2)
Nhận xét. Phân tích (2) cho ta thấy, bất đẳng thức \(\left(a+b+c\right)\left(\frac{3a-b}{a^2+ab}+\frac{3b-c}{b^2+bc}+\frac{3c-a}{c^2+ca}\right)\le9\)
đúng với mọi a, b, c là số thực thỏa mãn \(ab+bc+ca\ge0.\)

\(P=\frac{a}{2b+2c-a}+\frac{b}{2c+2a-b}+\frac{c}{2a+2b-c}=\frac{a^2}{2ab+2ac-a^2}+\frac{b^2}{2bc+2ab-b^2}+\frac{c^2}{2ac+2bc-c^2}\)
vì a,b,c là 3 cạnh của 1 tam giác áp dụng bđt tam giác có:
\(\hept{\begin{cases}b+c>a\Rightarrow2b+2c>a\Rightarrow2ab+2ac>a^2\Rightarrow2ab+2ac-a^2>0\\c+a>b\Rightarrow2c+2a>b\Rightarrow2bc+2ab>b^2\Rightarrow2bc+2ab-b^2>0\\a+b>c\Rightarrow2a+2b>c\Rightarrow2ac+2bc>c^2\Rightarrow2ac+2bc-c^2>0\end{cases}}\)
\(\Rightarrow\frac{a^2}{2ab+2ac-a^2}+\frac{b^2}{2bc+2ab-b^2}+\frac{c^2}{2ac+2bc-c^2}>0\)áp dụng bđt cauchy schawazt dạng enge ta có:
\(\frac{a^2}{2ab+2ac-a^2}+\frac{b^2}{2bc+2ab-b^2}+\frac{c^2}{2ac+2bc-c^2}>=\)
\(\frac{\left(a+b+c\right)^2}{2ab+2ac-a^2+2bc+2ab-b^2+2ac+2bc-c^2}=\frac{\left(a+b+c\right)^2}{4ab+4ac+4bc-\left(a^2+b^2+c^2\right)}\left(1\right)\)
vì \(a^2+b^2+c^2>=ab+ac+bc\Rightarrow4ab+4ac+4bc-\left(a^2+b^2+c^2\right)< =\)
\(4ab+4ac+4bc-\left(ab+ac+bc\right)\)mà \(\left(a+b+c\right)^2>0\)
\(\Rightarrow\frac{\left(a+b+c\right)^2}{4ab+4ac+4bc-\left(a^2+b^2+c^2\right)}>=\frac{\left(a+b+c\right)^2}{4ab+4ac+4bc-\left(ab+ac+bc\right)}\)(2)
\(=\frac{\left(a+b+c\right)^2}{4ab+4ac+4bc-ab-ac-bc}=\frac{\left(a+b+c\right)^2}{3ab+3ac+3bc}=\frac{a^2+b^2+c^2+2ab+2ac+2bc}{3ab+3ac+3bc}\)
\(>=\frac{ab+ac+bc+2ab+2ac+2bc}{3ab+3ac+3bc}=\frac{3ab+3ac+3bc}{3ab+3ac+3bc}=1\)(3)
từ (1)(2)(3)\(\Rightarrow\frac{a^2}{2ab+2ac-a^2}+\frac{b^2}{2bc+2ab-b^2}+\frac{c^2}{2ac+2bc-c^2}>=1\)
\(\Rightarrow P=\frac{a}{2b+2c-a}+\frac{b}{2c+2a-b}+\frac{c}{2a+2b-c}>=1\)
dấu = xảy ra khi a=b=c
vậy min P là 1 khi a=b=c

làm lại dong cuối:\(A\ge\frac{2}{c}+\frac{4}{b}+\frac{6}{a}\)
Mà:\(2c+b=abc\Rightarrow a=\frac{2c+b}{cb}=\frac{2}{b}+\frac{1}{c}\)
\(\Rightarrow2a=\frac{4}{b}+\frac{2}{c}\)
\(\Rightarrow A\ge2a+\frac{6}{a}\)
Ta có:\(A=\left(\frac{1}{b+c-a}+\frac{1}{a+c-b}\right)+2\left(\frac{1}{b+c-a}+\frac{1}{a+b-c}\right)\)
\(+3\left(\frac{1}{a+c-b}+\frac{1}{a+b-c}\right)\)
\(\ge\frac{2}{c}+\frac{4}{b}+\frac{6}{c}\) (Do a,b,c là 3 cạnh của tam giác nên:\(\hept{\begin{cases}a+b-c>0\\a+c-b>0\\c+b-a>0\end{cases}}\)
\(=\frac{6}{a}+2a\ge4\sqrt{3}\left(cosi\right)\left(a>0\right)\)
Dấu = xảy ra khi:
\(a=b=c=\sqrt{3}\)
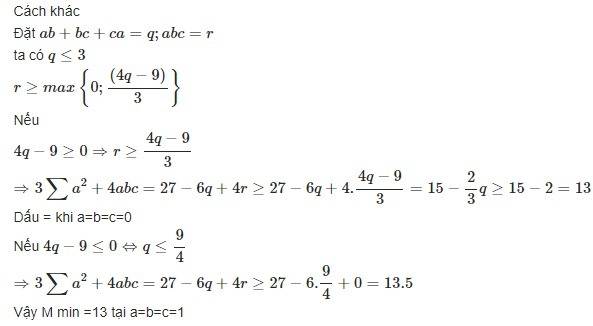
Ta dễ dàng chứng minh:
\(0< a,b,c\le\frac{3}{2}\)
Áp dụng BDT cô si cho ba số dương ta có:
\(\left(\frac{3}{2}-a\right)+\left(\frac{3}{2}-b\right)+\left(\frac{3}{2}-c\right)\ge3\sqrt[3]{\frac{3}{2}-a)(\frac{3}{2}-b)(\frac{3}{2}-c)}\)
\(\Leftrightarrow\left(\frac{1}{2}\right)^3\ge\frac{3}{2}-a)(\frac{3}{2}-b)(\frac{3}{2}-c)\)
\(\Leftrightarrow\frac{1}{8}\ge\frac{27}{8}-\frac{9}{4}\left(a+b+c\right)+\frac{3}{2}\left(ab+bc+ac\right)-abc\)
\(\Leftrightarrow\frac{1}{8}\ge-\frac{27}{8}+\frac{3}{2}\left(ab+bc+ac\right)-abc\)
\(\Leftrightarrow4abc\ge-14+6\left(ab+bc+ac\right)\)
\(\Leftrightarrow3a^2+3b^2+3c^2+4abc\ge13\)