
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Với a > 0, b > 0, c > 0, d > 0 ta có:
a < b ⇒ ac < bc (1)
c < d ⇒ bc < bd (2)
Từ (1) và (2) suy ra: ac < bd.

Ta có: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-2ab+b^2\Leftrightarrow a^2+b^2\ge2ab\)
Vì a ; b là các số dương nên chia cả 2 vế cho a;b ta được \(\frac{a}{b}+\frac{b}{a}\ge2\)
Đẳng thức xảy ra khi a = b
..
Ta có :\(\frac{a}{b}+\frac{b}{a}=\frac{a^2+b^2}{ab}\) \(\left(1\right)\)
Mà \(\left(a+b\right)^2>0\Rightarrow a^2+2ab+b^2>0\)
\(\Rightarrow a^2+b^2>2ab\)
\(\Rightarrow\frac{a^2+b^2}{ab}>\frac{2ab}{ab}\)
\(\Rightarrow\frac{a^2+b^2}{ab}>2\)\(\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{a}{b}+\frac{b}{a}>2\left(đpcm\right)\)
chúc bạn hok tốt

Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
⇒ a 2 + b 2 - 2 a b + 2 a b ≥ 2 a b ⇒ a 2 + b 2 ≥ 2 a b (*)
a > 0, b > 0 ⇒ a.b > 0 ⇒ 1/ab > 0
Nhân hai vế của (*) với 1/ab ta có:
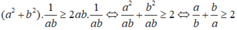

Sửa đề : ( a + b ) ( b + c ) ( c + a ) = 8abc
Giải :
Áp dụng bất đẳng thức AM - GM cho 2 số dương , ta có :
\(\hept{\begin{cases}a+b\ge2\sqrt{ab}\\b+c\ge2\sqrt{bc}\\c+a\ge2\sqrt{ca}\end{cases}}\)
Nhân vế với vế của 3 bất đẳng thức trên ta được :
\(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8abc\)
Dấu bằng xảy ra khi và chỉ khi a = b = c
Vì a,b,c là các số thực dương
nên áp dụng bất đẳng thức Cauchy ta có :
\(a+b\ge2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
\(c+a\ge2\sqrt{ca}\)
Nhân vế với vế
=> \(\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge2\sqrt{ab}\cdot2\sqrt{bc}\cdot2\sqrt{ca}=8\sqrt{a^2b^2c^2}=8\left|abc\right|=8abc\)
( do a,b,c là các số thực dương )
Đẳng thức xảy ra <=> a = b = c
=> đpcm

Câu hỏi của Adminbird - Toán lớp 7 - Học toán với OnlineMath

a) Áp dụng BĐT côsi ta có:\(\frac{a}{b}+\frac{b}{a}>=2\cdot\sqrt[2]{\frac{a}{b}\cdot\frac{b}{a}}=2\)
b)bạn nhân hết ra rồi áp dụng BĐT cối là được!!!!

Sửa đề: \(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge9\)
\(\Leftrightarrow3+\frac{a}{b}+\frac{a}{c}+\frac{b}{a}+\frac{b}{c}+\frac{c}{a}+\frac{c}{b}\ge9\)
\(\Leftrightarrow\left(\frac{a}{b}-2+\frac{b}{a}\right)+\left(\frac{a}{c}-2+\frac{c}{a}\right)+\left(\frac{b}{c}-2+\frac{c}{b}\right)\ge0\)
\(\Leftrightarrow\left(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\right)^2+\left(\sqrt{\frac{a}{c}}-\sqrt{\frac{c}{a}}\right)^2+\left(\sqrt{\frac{b}{c}}-\sqrt{\frac{c}{b}}\right)^2\ge0\)
Cái này đúng vậy ta có điều phải chứng minh
\(\left(a-b\right)^2\ge0\)\(\Leftrightarrow a^2+b^2-2ab\ge0\)\(\Leftrightarrow a^2+b^2\ge0\)
\(\Rightarrow\frac{a^2+b^2}{ab}\ge\frac{2ab}{ab}\)\(\Leftrightarrow\frac{a}{b}+\frac{b}{a}\ge2\)
Sửa để: \(\frac{a}{b}+\frac{b}{a}\ge2\)
\(\Leftrightarrow\left(\sqrt{\frac{a}{b}}-\sqrt{\frac{b}{a}}\right)^2\ge0\)