Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1/a + 1/b + 1/c = 1/a+b+c => \(\frac{ab+bc+ac}{abc}\)= \(\frac{1}{a+b+c}\)=> ( ab + bc + ac ) =abc => a2b +ab2 +bc2+b2c+ac2+a2c +3abc = abc
=> a2b+ab2+bc2+ac2+a2c+b2c+abc+abc=0 . Sau đó,bạn phân tích được là : (a+c)(b+c)(a+b)=0 => a=-c hoặc a=-b hoặc b=-c
Vậy trong ba số a,b,c có hai số đối nhau(đpcm).
Câu hỏi của Nguyễn Đa Vít - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo phần sau tại link trên!
chứng minh:(a+b+c)(1/a+1/b+1/c)<=10 nha mn. nhanh hộ mình
Không mất tính tổng quát giả sử a≥b≥c\(\Rightarrow \left ( a-b \right )\left ( b-c \right )\geq 0\)
\(\Rightarrow ab+bc\geq b^{2}+ac\)
=>\(\frac{a}{c}+1\geq \frac{b}{c}+\frac{a}{b}\) ; \(\frac{c}{a}+1\geq \frac{b}{a}+\frac{c}{b}\)
=>\(\frac{a}{b}+\frac{b}{c}+\frac{c}{b}+\frac{b}{a}\leq \frac{a}{c}+\frac{c}{a}+2=>\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\leq 2+2(\frac{a}{c}+\frac{c}{a})\)
Đặt \(x=\frac{a}{c},\)ta có 2 >= x >= 1 nên x + 1 /x <=5/2 => \(2 + 2 ( a/c + c/a)\)<= 7 => \(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}+\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\)<=7 => đpcm
Ta chứng minh BĐT
( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9
Áp dụng BĐT Cô – si cho hai số dương ta có:
a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng
= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3
Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có 1 + b 2 ≥ 2 b
Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )
Tương tự ta có:
b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )
Cộng từng vế của (1), (2) và (3) ta có:
a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3
a) thay m=-1 ta được
\(\left\{{}\begin{matrix}x+y=0\\-x-y=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x+y=0\\x+y=0\end{matrix}\right.\)
=> hpt vô nghiệm
b)hpt trên có vô số nghiệm <=>\(\dfrac{1}{m}=\dfrac{-m}{-1}=\dfrac{0}{m+1}\)(vô lí)
hpt trên chỉ có nghiệm duy nhất<=>\(\dfrac{1}{m}\ne\dfrac{-m}{-1}\)
<=>\(\dfrac{1}{m}\ne\dfrac{m}{1}\)
<=>\(m^2\ne1< =>m\ne\pm1\left(đpcm\right)\)
Với ab = 1 , a + b ¹ 0, ta có:
P = a 3 + b 3 ( a + b ) 3 ( a b ) 3 + 3 ( a 2 + b 2 ) ( a + b ) 4 ( a b ) 2 + 6 ( a + b ) ( a + b ) 5 ( a b ) = a 3 + b 3 ( a + b ) 3 + 3 ( a 2 + b 2 ) ( a + b ) 4 + 6 ( a + b ) ( a + b ) 5 = a 2 + b 2 − 1 ( a + b ) 2 + 3 ( a 2 + b 2 ) ( a + b ) 4 + 6 ( a + b ) 4 = ( a 2 + b 2 − 1 ) ( a + b ) 2 + 3 ( a 2 + b 2 ) + 6 ( a + b ) 4 = ( a 2 + b 2 − 1 ) ( a 2 + b 2 + 2 ) + 3 ( a 2 + b 2 ) + 6 ( a + b ) 4 = ( a 2 + b 2 ) 2 + 4 ( a 2 + b 2 ) + 4 ( a + b ) 4 = ( a 2 + b 2 + 2 ) 2 ( a + b ) 4 = ( a 2 + b 2 + 2 a b ) 2 ( a + b ) 4 = ( a + b ) 2 2 ( a + b ) 4 = 1
Vậy P = 1, với ab = 1 , a+b ¹ 0.
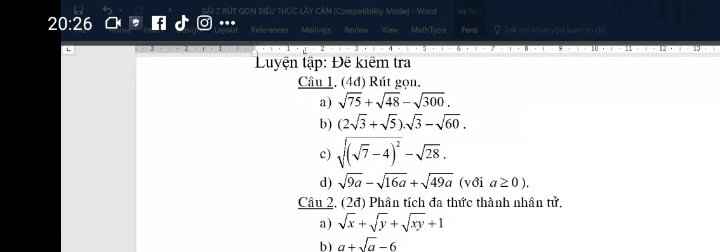
Câu 1:
b: Ta có: \(\left(2\sqrt{3}+\sqrt{5}\right)\cdot\sqrt{3}-\sqrt{60}\)
\(=6+\sqrt{15}-2\sqrt{15}\)
\(=6-\sqrt{15}\)
c: Ta có: \(\sqrt{\left(\sqrt{7}-4\right)^2}-\sqrt{28}\)
\(=4-\sqrt{7}-2\sqrt{7}\)
\(=4-2\sqrt{7}\)
cả 2 lớp có số học sinh là :
22+23= 45 ( hs )
đáp số 45 học sinh
giải
cả hai lớp có số học sinh là :
23 + 22 = 45 ( học sinh )
Đáp số : 45 học sinh
a) Xét (d): y = -2x + 3 có a = -2; b = 3
(d’) : y = 3x – 1 có a’ = 3 ; b’ = -1.
Có a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 
có nghiệm duy nhất.
b) 
Xét (d): 
có a = 
; b = 3
(d’): 
có a’ = 
; b’ = 1.
Có a = a’; b ≠ b’ ⇒ (d) // (d’)
⇒ Hệ phương trình 
vô nghiệm.
c) Ta có: 
Xét (d): y = 
x có a = 
; b = 0
(d’) : y = 
x có a’ = 
; b’ = 0
Ta có: a ≠ a’ ⇒ (d) cắt (d’)
⇒ Hệ 
có nghiệm duy nhất.
d) Ta có:
Ta có: a = a’=3; b = b’ = -3
Nhận thấy hai đường thẳng trên trùng nhau
⇒ Hệ phương trình có vô số nghiệm.
Kiến thức áp dụng
+ Xét hệ (I): 
Gọi (d): ax + by = c và (d’): a’x + b’y = c’.
Số nghiệm của hệ (I) phụ thuộc vào vị trí tương đối của (d) và (d’).
(d) cắt (d’) ⇒ hệ (I) có nghiệm duy nhất.
(d) // (d’) ⇒ hệ (I) vô nghiệm
(d) ≡ (d’) ⇒ hệ (I) có vô số nghiệm.
+ Cho đường thẳng (d): y = ax + b và (d’): y = a’x + b’.
(d) cắt (d’) ⇔ a ≠ a’
(d) // (d’) ⇔ a = a’ và b ≠ b’
(d) trùng (d’) ⇔ a = a’ và b = b’.