Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 3x^3 -10x+3 =(3x-1)(x-3)
| x | -vc | 1/3 | 5/4 | 3 | +vc | |||||||||
| 3x-1 | - | 0 | + | + | + | + | + | |||||||
| x-3 | - | - | - | - | - | 0 | + | |||||||
| 4x-5 | - | - | - | 0 | + | + | + | |||||||
| VT | - | 0 | + | 0 | - | 0 | + |
Kết luận
VT< 0 {dấu "-"} khi x <1/3 hoắc 5/4<x<3
VT>0 {dấu "+"} khi x 1/3<5/4 hoặc x> 3
VT=0 {không có dấu} khi x={1/3;5/4;3}

a: 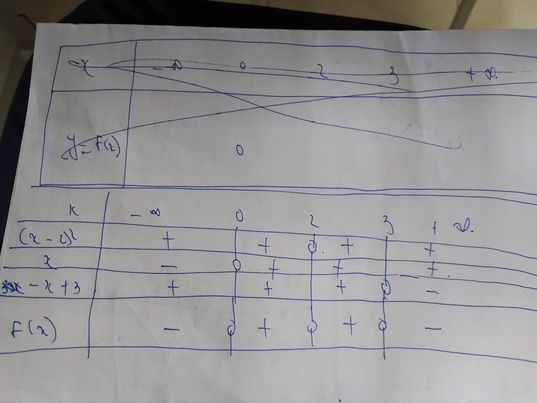
b: 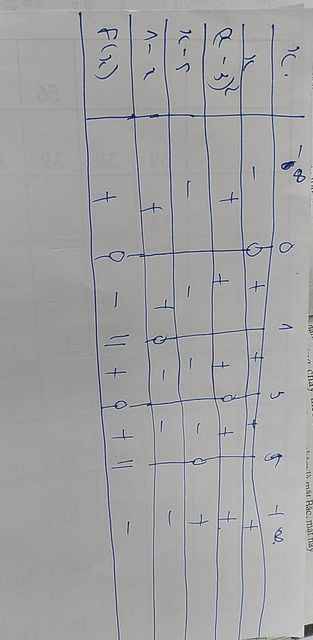
c: Đặt f(x)=0
=>-x^2+x+6=0
=>x^2-x-6=0
=>x=3 hoặc x=-2
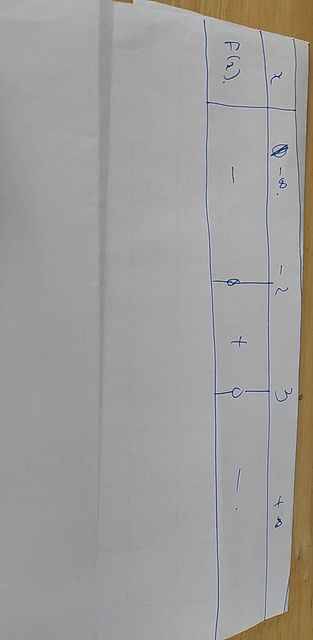
d: 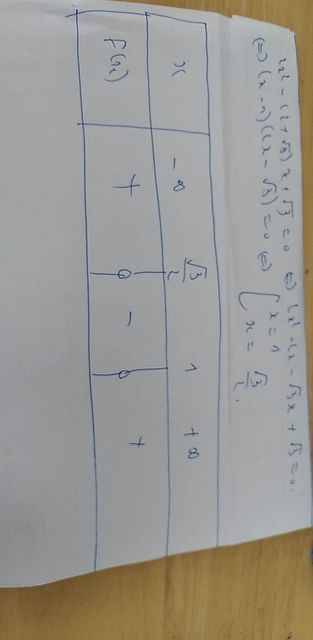

a) Ta lập bảng xét dấu
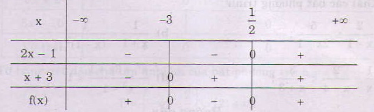
Kết luận: f(x) < 0 nếu - 3 < x <
f(x) = 0 nếu x = - 3 hoặc x =
f(x) > 0 nếu x < - 3 hoặc x > .
b) Làm tương tự câu a).
f(x) < 0 nếu x ∈ (- 3; - 2) ∪ (- 1; +∞)
f(x) = 0 với x = - 3, - 2, - 1
f(x) > 0 với x ∈ (-∞; - 3) ∪ (- 2; - 1).
c) Ta có: f(x) =
Làm tương tự câu b).
f(x) không xác định nếu x = hoặc x = 2
f(x) < 0 với x ∈ ∪
f(x) > 0 với x ∈ ∪ (2; +∞).
d) f(x) = 4x2 – 1 = (2x - 1)(2x + 1).
f(x) = 0 với x =
f(x) < 0 với x ∈
f(x) > 0 với x ∈ ∪

Lời giải:
\(f(x)=(-x+1)(x-2)>0\Leftrightarrow \left\{\begin{matrix} -x+1< 0\\ x-2< 0\end{matrix}\right.\) hay $1< x< 2$
hay $x\in (1;2)$
Đáp án D

a) f(x) = (x+2)(x-1)
f(x) > 0 với x < -2 hoặc x > 1
f(x) ≤ 0 với -2 ≤ x ≤ 1
b) y = 2x (x + 2) = 2(x+1)2 – 2
Bảng biến thiên:
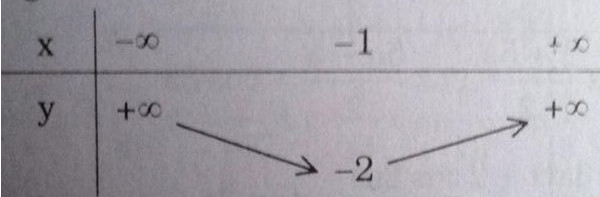
Hàm số : y = \(\left(x+2\right)\left(x+1\right)=\left(x+\dfrac{3}{2}\right)^2-\dfrac{1}{4}\)
Bảng biến thiên :
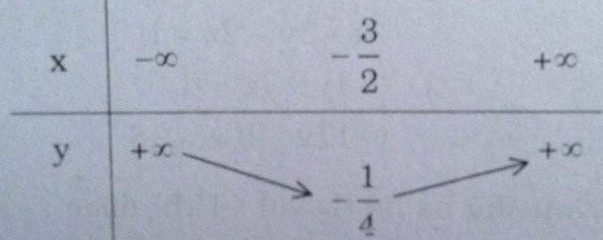
Đồ thị (C1) và (C2)
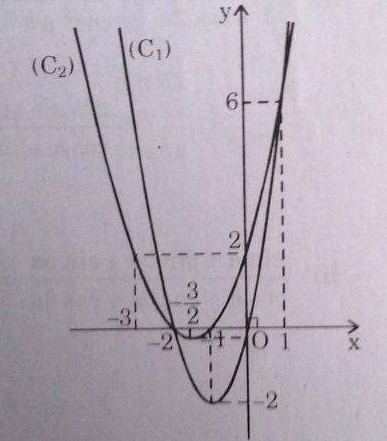
Hoành độ các giao điểm A và B của (C1) và (C2) là nghiệm của phương trình f(x) = 0 ⇔ x1 = -2, x2 = 1
⇔ A(-2, 0) , B(1, 6)
c) Giải hệ phương trình
\(\left\{{}\begin{matrix}\dfrac{ac-b^2}{4a}\\a\left(-2\right)^2+b\left(-2\right)+c=0\\a\left(1\right)^2+b\left(1\right)+c=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2,b=0,c=8\\a=-\dfrac{2}{9},b=\dfrac{16}{9},c=\dfrac{40}{9}\end{matrix}\right.\)
a/ \(f\left(x\right)=2x^2-2\left(a+b\right)x+a^2+b^2\)
\(=\frac{1}{2}\left[4x^2-4\left(a+b\right)x+\left(a+b\right)^2\right]+\frac{1}{2}a^2+\frac{1}{2}b^2-ab\)
\(=\frac{1}{2}\left(2x-a-b\right)^2+\frac{1}{2}\left(a-b\right)^2\ge\frac{1}{2}\left(a-b\right)^2\)
Dấu "=" xảy ra khi \(x=\frac{a+b}{2}\)
b/ \(f\left(x\right)=3x^2-2\left(a+b+c\right)x+a^2+b^2+c^2\)
\(=\frac{1}{3}\left[9x^2-6\left(a+b+c\right)x+\left(a+b+c\right)^2\right]+\frac{2}{3}\left(a^2+b^2+c^2\right)-\frac{2}{3}\left(ab+bc+ca\right)\)
\(=\frac{1}{3}\left(3a-a-b-c\right)^2+\frac{2}{3}\left(a^2+b^2+c^2-ab-bc-ca\right)\)
\(\Rightarrow f\left(x\right)_{min}=\frac{2}{3}\left(a^2+b^2+c^2-ab-bc-ca\right)\) khi \(x=\frac{a+b+c}{3}\)