K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

LS
17 tháng 4 2017
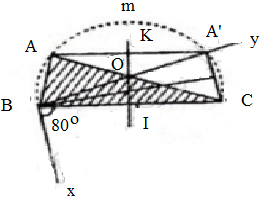
Trình tự dựng gồm các bước sau:
- Dựng đoạn thẳng BC = 6cm
- Dựng cung chứa góc 80 trên đoạn thẳng BC (cung BmC).
- Trên đường vuông góc với BC tại I(I là trung điểm BC), chọn điểm K sao cho IK = 2cm. Từ K dựng đường thẳng vuông góc với IK. Đường thẳng này cắt cung chứa góc BmC tại A và A'.
ΔABC (hoặc ΔA'BC) là tam giác thỏa mãn yêu cầu đề bài.
Kẻ đường cao BD (D thuộc AC)
Trong tam giác vuông ABD:
\(cosA=\dfrac{AD}{AB}\Rightarrow AD=AB.cosA=12.cos30^0=6\sqrt{3}\)
\(sinA=\dfrac{BD}{AB}\Rightarrow BD=AB.sinA=12.sin30^0=6\)
\(\Rightarrow CD=AC-AD=8\)
Áp dụng định lý Pitago cho tam giác vuông BCD:
\(BC=\sqrt{BD^2+CD^2}=10\left(cm\right)\)