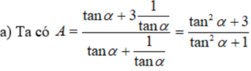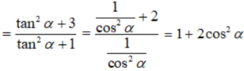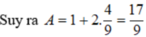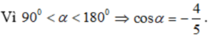Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

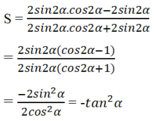
Đáp án: A
Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.


Chọn C.
Ta có tan α – cotα = 1

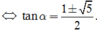
Do ![]() suy ra tanα < 0 nên
suy ra tanα < 0 nên
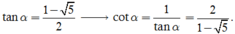
Thay
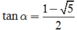 và
và 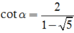
vào P ta được
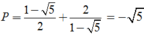

Tham khảo:
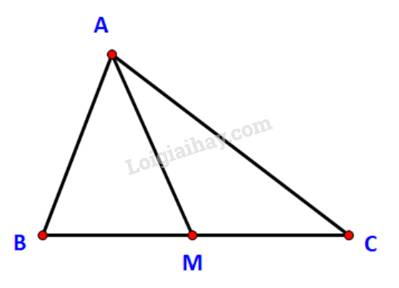
a) Ta có: \(\widehat {AMB} + \widehat {AMC} = {180^o}\)
\( \Rightarrow \cos \widehat {AMB} = - \cos \widehat {AMC}\)
Hay \(\cos \widehat {AMB} + \cos \widehat {AMC} = 0\)
b) Áp dụng định lí cos trong tam giác AMB ta có:
\(\begin{array}{l}A{B^2} = M{A^2} + M{B^2} - 2MA.MB\;\cos \widehat {AMB}\\ \Leftrightarrow M{A^2} + M{B^2} - A{B^2} = 2MA.MB\;\cos \widehat {AMB}\;\;(1)\end{array}\)
Tương tự, Áp dụng định lí cos trong tam giác AMB ta được:
\(\begin{array}{l}A{C^2} = M{A^2} + M{C^2} - 2MA.MC\;\cos \widehat {AMC}\\ \Leftrightarrow M{A^2} + M{C^2} - A{C^2} = 2MA.MC\;\cos \widehat {AMC}\;\;(2)\end{array}\)
c) Từ (1), suy ra \(M{A^2} = A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}\;\)
Từ (2), suy ra \(M{A^2} = A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}\;\)
Cộng vế với vế ta được:
\(2M{A^2} = \left( {A{B^2} - M{B^2} + 2MA.MB\;\cos \widehat {AMB}} \right)\; + \left( {A{C^2} - M{C^2} + 2MA.MC\;\cos \widehat {AMC}} \right)\;\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - M{B^2} - M{C^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MC\;\cos \widehat {AMC}\)
Mà: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\( \Rightarrow 2M{A^2} = A{B^2} + A{C^2} - {\left( {\frac{{BC}}{2}} \right)^2} - {\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\cos \widehat {AMB} + 2MA.MB\;\cos \widehat {AMC}\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - 2.{\left( {\frac{{BC}}{2}} \right)^2} + 2MA.MB\;\left( {\cos \widehat {AMB} + \;\cos \widehat {AMC}} \right)\)
\( \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\)
\(\begin{array}{l} \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\) (đpcm)
Cách 2:
Theo ý a, ta có: \(\cos \widehat {AMC} = - \cos \widehat {AMB}\)
Từ đẳng thức (1): suy ra \(\cos \widehat {AMB} = \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
\( \Rightarrow \cos \widehat {AMC} = - \cos \widehat {AMB} = - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}\)
Thế \(\cos \widehat {AMC}\)vào biểu thức (2), ta được:
\(M{A^2} + M{C^2} - A{C^2} = 2MA.MC.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\)
Lại có: \(MB = MC = \frac{{BC}}{2}\) (do AM là trung tuyến)
\(\begin{array}{l} \Rightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = 2MA.MB.\left( { - \frac{{M{A^2} + M{B^2} - A{B^2}}}{{2.MA.MB}}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} = - \left( {M{A^2} + M{B^2} - A{B^2}} \right)\\ \Leftrightarrow M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{C^2} + M{A^2} + {\left( {\frac{{BC}}{2}} \right)^2} - A{B^2} = 0\\ \Leftrightarrow 2M{A^2} - A{B^2} - A{C^2} + {\frac{{BC}}{2}^2} = 0\\ \Leftrightarrow 2M{A^2} = A{B^2} + A{C^2} - {\frac{{BC}}{2}^2}\\ \Leftrightarrow M{A^2} = \frac{{A{B^2} + A{C^2} - {{\frac{{BC}}{2}}^2}}}{2}\\ \Leftrightarrow M{A^2} = \frac{{2\left( {A{B^2} + A{C^2}} \right) - B{C^2}}}{4}\end{array}\)

c o t 2 α = 1 / ( sin 2 α ) – 1 = 25 / 20 – 1 = 1/4 ⇒ cotα = ±1/2.
Vì 3π/2 < α < 2π nên cotα < 0. Vậy cotα = (-1)/2.
Đáp án: C

Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!