Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

#)Giải :
Vì AD,BE,CF là ba đường phân giác
\(\Rightarrow\frac{FA}{FB}=\frac{CA}{CB};\frac{DB}{DC}=\frac{AB}{AC};\frac{EC}{EA}=\frac{BC}{BA}\)
\(\Rightarrow\frac{FA}{FB}.\frac{DB}{DC}.\frac{EC}{EA}=\frac{CA.AB.BC}{CB.AC.BA}=1\left(đpcm\right)\)
Tham khảo tại :
Câu hỏi của Phạm Hoàng - Toán lớp 8 | Học trực tuyến
< https://h.vn/hoi-dap/question/555217.html >
~ chúc bn học tốt~

AD,BE,CF là phân giác
ta có \(\dfrac{FA}{FB}.\dfrac{DB}{DC}.\dfrac{EC}{EA}=\dfrac{AB}{AC}.\dfrac{BC}{BA}.\dfrac{CA}{CB}\)
do \(\dfrac{FA}{FB}=\dfrac{CA}{CB};\dfrac{DB}{DC}=\dfrac{AB}{AC};\dfrac{EC}{EA}=\dfrac{BC}{BA}\)
mà \(\dfrac{AB}{AC}.\dfrac{BC}{BA}.\dfrac{CA}{CB}=1\)
nên \(\dfrac{FA}{FB}.\dfrac{DB}{DC}.\dfrac{EC}{EA}=1\)

A D E I B C M N
a) Xét \(\Delta ABD\) và \(\Delta ACE\) ,có :
AD = AE ( Tam giác ADE cân tại A )
\(\widehat{ADE}=\widehat{AED}\) ( Tam giác ADE cân tại A )
BD = CE ( gt )
=> \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
=> AB = AC
=> \(\Delta ABC\) cân tại A
b) Xét \(\Delta BMD\) và \(\Delta CNE\) ,có :
BD = CE ( gt )
\(\widehat{BMD}=\widehat{CNE}=90^0\)
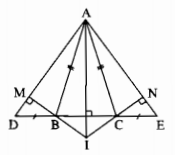
a) Xét ∆ADE cân tại A nên góc D = góc E
Xét ∆ABD và ∆ACE, ta có:
AD = AE (gt)
góc D = góc E (chứng minh trên)
DB = EC (gt)
Suy ra: ∆ABD = ∆ACE (c.g.c)
Suy ra: AB = AC (hai cạnh tương ứng)
Vậy ∆ABC cân tại A.
b) Xét hai tam giác vuông BMD và CNE, ta có:
góc BMD=góc CNE=90o
BD = CE (gt)
góc D = góc E (chứng minh trên)
Suy ra: ∆BMD = ∆CNE (cạnh huyền, góc nhọn)
Suy ra: BM = CN (hai cạnh tương ứng)
c) Ta có: ∆BMD = ∆CNE (chứng minh trên)
Suy ra: góc DBM=góc ECN (hai góc tương ứng)
góc DBM=góc IBC (đối đỉnh)
góc ECN = góc ICB (đối đỉnh)
Suy ra: góc IBC=góc ICB hay ∆IBC cân tại I.
d) Xét ∆ABI và ∆ACI, ta có:
AB = AC (chứng minh trên)
IB = IC (vì ∆IBC cân tại I)
AI cạnh chung
Suy ra: ∆ABI = ∆ACI (c.c.c) ⇒ góc BAI=góc CAI (hai góc tương ứng)
Vậy AI là tia phân giác của góc BAC
Áp dụng t/c đường phân giác, ta có:
\(\dfrac{AB}{AC}=\dfrac{BD}{CD}\) ( 1 )
\(\dfrac{BC}{BA}=\dfrac{EC}{EA}\) ( 2 )
\(\dfrac{CA}{CB}=\dfrac{FA}{FB}\) ( 3 )
Nhân từng vế (1);(2);(3) ta được:
\(\dfrac{AB}{AC}\times\dfrac{BC}{BA}\times\dfrac{CA}{CB}=\dfrac{BD}{CD}\times\dfrac{EC}{EA}\times\dfrac{FA}{FB}\)
\(\Leftrightarrow1=\dfrac{BD}{CD}\times\dfrac{EC}{EA}\times\dfrac{FA}{FB}\)
ADAD là đường phân giác ˆA→ABAC=DBDCA^→ABAC=DBDC
BEBE là đường phân giác ˆB→BCBA=ECEAB^→BCBA=ECEA
CFCF là đường phân giác ˆC→CACB=FAFBC^→CACB=FAFB
→DBDC.ECEA.FAFB=ABAC.BCBA.CACB=AB.BC.CAAC.BA.CB=1