Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

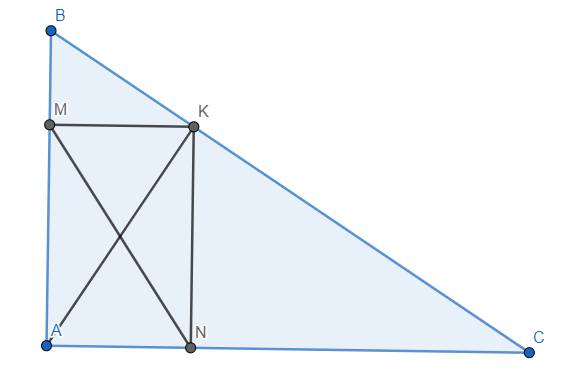
a) Tam giác AKB vuông tại K có đường cao KM nên \(AK^2=AM.AB\)
Chứng minh tương tự, ta có \(AK^2=AN.AC\)
Từ đó suy ra \(AM.AB=AN.AC\) (đpcm)
b) Tam giác KMN vuông tại K nên \(KM^2+KN^2=MN^2\)
Dễ thấy tứ giác AMKN là hình chữ nhật, suy ra \(AK=MN\). Từ đó \(KM^2+KN^2=AK^2\).
Tam giác ABC vuông tại A, đường cao AK nên \(AK^2=KB.KC\)
Thế thì \(KM^2+KN^2=KB.KC\) (đpcm)
c) Tam giác AKB vuông tại K, có đường cao KM nên \(AM.BM=KM^2\)
Tương tự, ta có \(AN.CN=KN^2\)
Từ đó \(AM.BM+AN.CN=KM^2+KN^2\)
Theo câu b), \(KM^2+KN^2=KB.KC\)
Do đó \(AM.BM+AN.CN=KB.KC\) (đpcm)

c: Xét ΔAHB vuông tại H có HI là đường cao
nên \(AI\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HK là đường cao
nên \(AK\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AI\cdot AB=AK\cdot AC\)

a: Xét (O) có
ΔAHM nội tiếp
AH là đường kính
=>ΔAMH vuông tại M
Xét (O) có
ΔANH nội tiếp
AH là đường kính
=>ΔANH vuông tại N
ΔHAB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔHCA vuông tại H có HN là đường cao
nên AN*AC=AH^2
b: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>góc ANM=góc AHM=góc ABC
=>góc MBC+góc MNC=180 độ
=>NMBC là tứ giác nội tiếp