Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

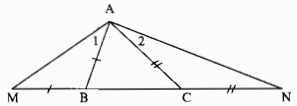
Trong ∆ABC có AB < AC
⇒ góc ABC= góc ACB (đối diện cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt)
⇒ góc ∆ABM cân tại B
⇒ góc M = góc A1(tính chất tam giác cân)
Trong ∆ABM ta có có góc ngoài tại đỉnh B
góc ABC= góc M+ góc A1
Suy ra: góc M=12 góc ABC (2)
Ta có: AC = CN (gt)
⇒ ∆CAN cân tại C⇒ góc N= góc A2 (tính chất tam giác cân)
Trong ∆CAN ta có góc ACB là góc ngoài tại đỉnh C.
⇒góc ACB= góc N+ góc A2
Suy ra: góc N=12 góc ACB (3)
Từ (1), (2) và (3) suy ra: góc M > góc N
b) Trong ∆AMN ta có: góc M> góc N

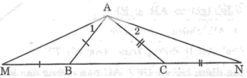
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .

a) Xét tg ABM và ACM có :
AB=AC(gt)
AM-cạnh chung
MB=MB(gt)
=> Tg ABM=ACM(c.c.c)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
=> AM là tia pg góc A (đccm)
b) Xét tg BNC và DNC có :
BC=CD(gt)
\(\widehat{DCN}=\widehat{BCN}\left(gt\right)\)
NC-cạnh chung
=> Tg BNC=DNC(c.g.c)
\(\Rightarrow\widehat{CND}=\widehat{CNB}=\frac{\widehat{DNB}}{2}=\frac{180^o}{2}=90^o\)
\(\Rightarrow CN\perp BD\left(đccm\right)\)
c) Có : AB=AC(gt)
=> Tg ABC cân tịa A
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)(1)
- Do tg BNC=DNC(cmt)
\(\widehat{ABC}=\widehat{BDC}\)(2)
- Từ (1) và (2)\(\Rightarrow\widehat{BDC}=\widehat{ACB}\)
- Có : \(\widehat{ADC}+\widehat{BDC}=180^o\)
\(\widehat{ACB}+\widehat{BCE}=180^o\)
Mà : \(\widehat{BDC}=\widehat{ACB}\left(cmt\right)\)
\(\Rightarrow\widehat{BCE}=\widehat{ADC}\left(đccm\right)\)
d) Xét tg ACD và EBC có :
BC=CD(gt)
DA=CE(gt)
\(\widehat{BCE}=\widehat{ADC}\left(cmt\right)\)
=> Tg ACD=EBC(c.g.c)
=> AC=BE
Mà AC=AB(gt)
=> BE=AB (đccm)
#H

a/ Xét ΔABM;ΔACMΔABM;ΔACM có :
⎧⎩⎨⎪⎪AB=ACBˆ=CˆMB=MC{AB=ACB^=C^MB=MC
⇔ΔAMB=ΔAMC(c−g−c)⇔ΔAMB=ΔAMC(c−g−c)
b/ Xét ΔBHM;ΔCKMΔBHM;ΔCKM có :
⎧⎩⎨⎪⎪⎪⎪BHMˆ=CKMˆ=900Bˆ=CˆMB=MC{BHM^=CKM^=900B^=C^MB=MC
⇔ΔBHM=ΔCKM(ch−gn)⇔ΔBHM=ΔCKM(ch−gn)
⇔BH=CK