Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác ABE và tam giác ADE
AE chung
góc BAE = góc DAE(AE la tia phân giác của góc E)
AB = AD ( gt)
=> tam giác ABE = tam giac DAE ( c.g.c)
b) xét tam giác ABI và tam giác ADI
AI chung
góc BAE = góc DAE
tam giác ABI=tam giác ADI
=> BI = DI ( 2 cạnh t/ứ )
=> I là trung điểm của BD

a) Ta có: góc ^ADC=180* -(^CAD+^C)
^BDA=180*-(^BAD+^B)
mà ^CAD=^BAD(giả thiết)
^C=^B(giả thiết)
--> ^ADC=^BDA
lại có:
^CAD=^BAD(gt)
AD chung
--> tam giác ABD=tam giác ACD

Hình tự vẽ nha bạn
a) Xét \(\Delta AHB\)và \(\Delta AKC\)có:
\(\hept{\begin{cases}\widehat{A}:chung\\AB=AC\left(gt\right)\\\widehat{AHB}=\widehat{AKC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta AHB=\Delta AKC\left(ch-gn\right)\)
=>AH=AK ( 2 cạnh tương ứng) -đpcm
b) Xét \(\Delta AKI\)và \(\Delta AHI\)có:
\(\hept{\begin{cases}AK=AH\\\widehat{AKI}=\widehat{AHI}\\AI:chung\end{cases}}\)
\(\Rightarrow\Delta AKI=\Delta AHI\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAK}=\widehat{IAH}\)( 2 góc tương ứng)
=> AI là ti phân giác góc KAH
Xét \(\Delta KAH\)cân tại A ( do AH=AK ) có AI là tia phân giác ứng cạnh KH
=> AI đồng thời là đường trung trực của cạnh KH (t/c) -đpcm
c) Kẻ CM \(\perp\)BE
Xét tứ giác BKCM có:
\(\hept{\begin{cases}\widehat{CKB}=90^0\\\widehat{KBM}=90^0\\\widehat{BMC}=90^0\end{cases}}\)
=> tứ giác BKCM là hình chữ nhật (dấu hiệu nhận biết)
=> BK=CM (t/c) (1)
Dễ dàng chứng minh đc: BK=CH (2)
Từ (1) và (2) có : CM=CH
Xét \(\Delta BHC\)và \(\Delta BMC\)có:
\(\hept{\begin{cases}CH=CM\\\widehat{BHC}=\widehat{BMC}\\CB:chung\end{cases}}\)
=> \(\Delta BHC=BMC\left(ch-cgv\right)\)
=> \(\widehat{CBH}=\widehat{CBM}\)(2 góc tương ứng)
=> BC là tia phân giác góc HBM
hay BC là tia phân giác HBE -đpcm
Chúc bạn học tốt!
d) Xét tam giác CME vuông tại M có CE là cạnh huyền
=>CE>CM (trong tam giác vuông cạnh huyền là cạnh lớn nhất)
mà CH=CM do \(\Delta CBH=\Delta CBM\)
=>CE>CH

a, Xét tam gác ABH và tam giác ACH có:
AB=AC (gt)
BH=CH
AH là cạnh chung
=> tam giác ABH=ACH ( c.c.c)
=> góc BAH = CAH ( hai góc tương ứng )
Vì tam giác ABC là tam giác cân mà AH vừa là trung điểm vừa là tia phân giác thì AH cũng là đường cao của ta giác ABC => AH vuông góc vs BC
b, Xét tam giác vuông ABH và tam giác vuông KCH có :
BH=CH (gt)
HK=HA (gt)
=> tam giác vuông ABH = tam giác vuông KCH ( hai cạnh góc vuông )
=> góc HAB = góc HKC ( hai góc tương ứng )
Vì góc HAB = góc HKC nên CK//AB ( cặp góc sole trong )

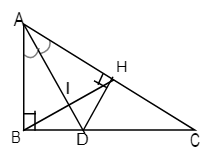
a) Xét ΔABD và ΔAHD có:
∠ABD = ∠AHD = 90 (gt)
Cạnh AD chung
∠BAD = ∠HAD (gt)
⇒ ΔABD = ΔAHD (ch - gn)
b) Xét ΔABC có:
∠B = 90o
⇒ ∠A + ∠C =90o
⇒ ∠C = 90o − ∠A = 90o − 60o = 30o
Vì AD là tia phân giác của ∠A (gt)
⇒ ∠BAD = ∠DAC = ∠A/2 = 60o/2 = 30o
⇒ ∠C = ∠DAC = 30o
⇒ ΔADC cân tại D
⇒ AD = DC
⇒ AH = HC (quan hệ giữa đường xiên và hình chiếu)
c) Xét ΔABD có :
AB < AD (cạnh góc vuông < cạnh huyền)
Mà AD = DC (cmt)
⇒ DC > AB

a) Xét tam giác ABD và tam giác HBD có :
góc ABD = góc HBD (BD là tia pg)
góc BAD = góc BHD=90 độ (gt)
BD là cạnh chung
=> Tam giác ABD = Tam giác HBD (CH-GN)
=> AD = DH ( 2 cạnh tương ứng )
b) Xét tam giác DHC có :
Góc DHC = 90 độ => DC là cạnh huyền => DC > DH
Ta lại có : AD=DH ( cm ở câu a )
=> DC>AD
a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD