Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: \(AM=MB=\dfrac{AB}{2}\)
\(AN=NC=\dfrac{AC}{2}\)
mà AB=AC
nên AM=MB=AN=NC
Xét ΔABN và ΔACM có
AB=AC
\(\widehat{BAN}\) chung
AN=AM
Do đó: ΔABN=ΔACM
=>BN=CM
b: Xét ΔMBC và ΔNCB có
MB=NC
MC=NB
BC chung
Do đó: ΔMBC=ΔNCB
=>\(\widehat{MCB}=\widehat{NBC}\)
=>\(\widehat{GBC}=\widehat{GCB}\)
=>ΔGBC cân tại G
c: Xét ΔABC có
BN,CM là các đường cao
BN cắt CM tại G
Do đó: G là trọng tâm của ΔABC
Xét ΔABC có
G là trọng tâm
AG cắt BC tại D
DO đó: \(AG=\dfrac{2}{3}AD=\dfrac{2}{3}\cdot3=2\left(cm\right)\)

Xét ΔABM và ΔACN có
AB=AC
góc BAM chung
AM=AN
=>ΔABM=ΔACN
=>BM=CN
Mình xin phép sửa đề:
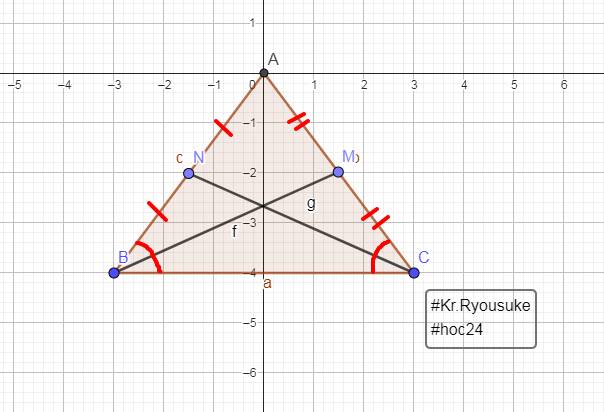
Cho tam giác ABC cân tại A , các đường trung tuyến BM và CN cắt nhau tại G
Chứng minh tam giác ABN = tam giác ACN , từ đó suy ra BM=CN
`------`
\(\text{GT | AB = AC, }\widehat{\text{B}}=\widehat{\text{C}}\)
\(\text{CM | BM = CN}\)
\(\text{BM là đường trung tuyến}\)
`->`\(\text{MA = MC (1)}\)
\(\text{CN là đường trung tuyến}\)
`->`\(\text{NA = NB (2)}\)
`\Delta ABC` cân tại A
`->`\(\widehat{\text{B}}=\widehat{\text{C}}\text{, AB = AC (3)}\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\)
`->`\(\text{NA = NB = MA = MC}\)
Xét `\Delta ABM` và `\Delta ACN`:
\(\left\{{}\begin{matrix}\text{BM = CN}\\\widehat{\text{B}}=\widehat{\text{C}}\\\text{BC chung}\end{matrix}\right.\)
`=> \Delta ABM = \Delta ACN (c-g-c)`
`->`\(\text{BM = CN (2 cạnh tương ứng).}\)

a) BE = DC, ΔBEC = ΔCDB.
Vì ΔABC cân tại A nên: AB = AC.
Ta lại có: AB = AE + EB mà AE = EB (gt)
AC = AD + DC mà AD = DC (gt)
⇒ AE = EB = AD = DC
Vậy BE = DC.
Xét ΔBEC và ΔCDB có:
BE = CD (cmt)
∠ABC = ∠ACB (ΔABC cân)
BC : cạnh chung.
Do đó: ΔBEC = ΔCDB (c.g.c)
b) ΔBGC cân.
Vì ΔBEC = ΔCDB (câu a)
⇒ ∠ECB = ∠DBC (hai góc tương ứng)
⇒ ΔBGC cân tại G.
Câu c và hình chờ xíu :v
c) BC <4GD
Kẻ trung tuyến AG ⇒ G là trọng tâm của ΔABC, mà ΔABC cân (gt) ⇒ AG là phân giác của ∠BAC (∠A1 = ∠A2)
AG cắt BC tại H (HB = HC)
Xét ΔABH và ΔACH có:
AB = AC (gt)
BH = HC (cmt)
AH : chung
Do đó: ΔABH = ΔACH (c.c.c)
⇒ ∠H1 = ∠H2 (hai góc tương ứng) Mà ∠H1 + ∠H2 = 180o
⇒ ∠H1 = ∠H2 = 180o : 2 = 90o hay AH ⊥ BC.
Vì ΔBGC cân tại G nên: GB = GC (hai cạnh đáy) Mà GB = 2GD
⇒ 4GD = DB + GC.
Xét ΔBGH vuông tại H, ta có: BG > BH (định lí) (1)
Xét ΔCGH vuông tại H, ta có: CG > CH (định lí) (2)
Từ (1) và (2) suy ra: BG + CG > BH + CH
Mà GB + CG = 4GD (cmt) và CB = BH + CH
⇒ 4GD > BC

a. trong tam giác cân 2 đường trung tuyến ở góc đáy bằng nhau nên CF=BE (1)
vì G là trọng tâm tam giác ABC nên GC=2/3 FC ;BG= 2/3 BE (2)
tu 1 va 2 suy ra CG=BG
suy ra tam giác BGC cân tại G
c. Xet tam giac AMB va tam giac AMC co
AB=AC
ABC=ACB
AM chung
suy ra tam giac AMB= tam giac AMC
suy ra MB=MC
Suy ra AM la trung tuyen
suy ra G thuộc đường thẳng AM
Suy ra A,G,M thẳng hàng
b. tren tia doi FE lay diem K sao cho EK=EF
xet tg AEF = tg CEK ( c.g.c )
suy ra BA song song KC, AF=FB=KC
nối B với K
xet tam giac FBK = tg CKB ( c.g.c )
suy ra FE song song BC
bán xoi tam 3 câu trước đi nhé để mik suy nghĩ câu d
câu d mik chứng minh phản chứng nếu bạn thấy sai chỗ nào bảo mik nhé
Vì G là trọng tâm nên GE=1/3BE suy ra 3GE=BE
TH1: nếu AE>3GE suy ra AE>BE
suy ra EC>BE
suy ra gEBC>gECB ( vô lý vì gECB=gEBC )
TH2: AE=3GE suy ra AE=BE
suy ra EC=BE
suy ra tg EBC can tai E
suy ra gEBC=gECB ( vo ly vi gECB=gFBC )
vay AE<3GE
Hì mik cùng bằng lớp bạn nên thấy mik làm sai thì chỉ bảo mik nha

â)xét tam giác abd và acd có
ab=ac(abc là tam giác cân )
ad chung
góc a1=a2(ad là tia phân giác góc a)
=>tam giác abd=acd(trường hợp cạnh-góc -cạnh)
b)vì tam giác abc=acd(câu a)=>bd=cd=>ad là trung tuyến cạnh bc
mà cf là đuong trung tuyển cạnh ba=>ad và cf cùng đi qua một điểm
=> g là trọng tâm
câu c mình vẫn chưa nghĩ ra được .xin lỗi nha
c) H là trung điểm của CD \(\Rightarrow\)DH=HC
mà EH vuông góc vs DC \(\Rightarrow\) EH là đường cao
\(\Rightarrow\)EH là đường trung trực của CD \(\Rightarrow\)ED=EC \(\Rightarrow\)tam giác DEC cân tại E
d) tam giác GBC cân tại G ( CM tương tự như trên )
\(\Rightarrow\) góc GBC =GCB
mà \(\widehat{B}=\widehat{C}\)(tam giác ABC cân tại A)
\(\widehat{GBD}+\widehat{ABE}=\widehat{B}\) ; \(\widehat{GCB}+\widehat{ACF}=\widehat{C}\)
\(\Rightarrow\) GÓC ABE = ACF
TAM GIÁC ABE = TAM GIÁC ACF (G.C.G)
\(\Rightarrow\) AE=AF
MÀ AF=1/2AB ( CF là đường trung tuyến ) ; AB=AC (tam giác ABC cân tại A )
\(\Rightarrow\) AE = 1/2 AC \(\Rightarrow\) E LÀ TRUNG ĐIỂM CỦA AC
\(\Rightarrow\) BE LÀ ĐƯỜNG TRUNG TUYẾN
mà G là trọng tâm của tam giác ABC
\(\Rightarrow\)BE đi qua G \(\Rightarrow\)3 điểm B,E,G thẳng hàng
Nãy làm rồi đang định gửi thì bận:vvv
a) Vì ∆ABC cân tại A => AB=AC
<=> \(\dfrac{1}{2}AB=\dfrac{1}{2}AC\Leftrightarrow BF=CE\)
Xét ∆BFC và ∆CEB:
BF=CE(cmt)
BC: cạnh chung
\(\widehat{FBC}=\widehat{ECB}\) (∆ABC cân tại A)
=> ∆BFC=∆CEB(c.g.c)
b) Vì theo câu a: ∆BFC=∆CEB
=> \(\widehat{FCB}=\widehat{EBC}\) (2 góc t/ứ)
=> ∆BCG cân tại G