Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAKB và ΔAKC có
AK chung
\(\hat{KAB}=\hat{KAC}\)
AB=AC
Do đó: ΔAKB=ΔAKC
=>KB=KC
=>K nằm trên đường trung trực của BC(1)
Ta có: O nằm trên đường trung trực của AB
=>OA=OB(2)
ta có: O nằm trên đường trung trực của AC
=>OA=OC(3)
Từ (2),(3) suy ra OB=OC
=>O nằm trên đường trung trực của BC(4)
Ta có: AB=AC
=>A nằm trên đường trung trực của BC(5)
Từ (1),(4),(5) suy ra A,O,K thẳng hàng
b: Xét ΔDBC và ΔECB có
\(\hat{DBC}=\hat{ECB}\) (ΔABC cân tại A)
BC chung
\(\hat{DCB}=\hat{EBC}\) (ΔOBC cân tại O)
Do đó: ΔDBC=ΔECB
=>DC=EB và DB=EC
Ta có: DB+AD=AB
EC+AE=AC
mà DB=EC và AB=AC
nên AD=AE
Gọi I là giao điểm của hai đường trung trực của các đoạn thẳng AD,AE
I nằm trên đường trung trực của AD
=>IA=ID(6)
I nằm trên đường trung trực của AE
=>IA=IE(7)
Từ (6),(7) suy ra IE=ID
OD=OE nên O nằm trên đường trung trực của ED(8)
IE=ID nên I nằm trên đường trung trực của ED(9)
AE=AD nên A nằm trên đường trung trực của ED(10)
Từ (8),(9),(10) suy ra A,I,O thẳng hàng
mà A,O,K thẳng hàng
nên A,I,O,K thẳng hàng
=>ĐPCM



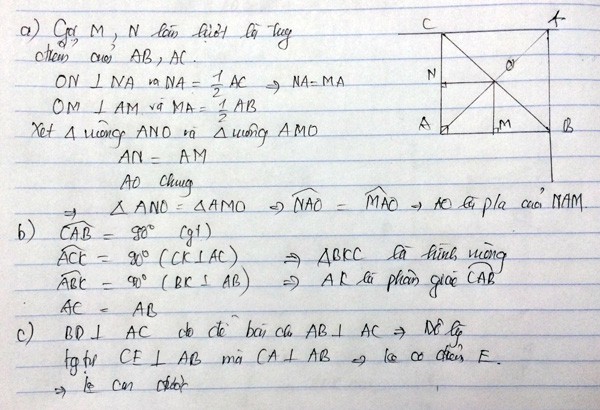
a) Ta có: O là giao điểm của hai đường trung trực của AB và AC(gt)
⇒O nằm trên đường trung trực của AB
⇒OA=OB(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: O là giao điểm của hai đường trung trực của AB và AC(gt)
⇒O nằm trên đường trung trực của AC
⇒OA=OC(tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OB=OC
hay O nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(4)
Xét ΔABK và ΔACK có
AB=AC(ΔABC cân tại A)
\(\widehat{BAK}=\widehat{CAK}\)(AK là tia phân giác của \(\widehat{BAC}\))
AK chung
Do đó: ΔABK=ΔACK(c-g-c)
⇒BK=CK(hai cạnh tương ứng)
hay K nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(5)
Từ (3), (4) và (5) suy ra A,O,K thẳng hàng(đpcm)