Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét tam giác ABD và tam giác HBD có :
góc ABD = góc HBD (BD là tia pg)
góc BAD = góc BHD=90 độ (gt)
BD là cạnh chung
=> Tam giác ABD = Tam giác HBD (CH-GN)
=> AD = DH ( 2 cạnh tương ứng )
b) Xét tam giác DHC có :
Góc DHC = 90 độ => DC là cạnh huyền => DC > DH
Ta lại có : AD=DH ( cm ở câu a )
=> DC>AD

a: Xét ΔABD và ΔACD có
AB=AC
AD chung
BD=CD
Do đó: ΔABD=ΔACD

5 )
tự vẽ hình nha bạn
a)
Xét tam giác ABM và tam giác ACM có :
AM cạnh chung
AB = AC (gt)
BM = CM (gt)
suy ra : tam giác ABM = tam giác ACM ( c-c-c)
suy ra : góc BAM = góc CAM ( 2 góc tương ứng )
Hay AM là tia phân giác của góc A
b)
Xét tam giác ABD và tam giác ACD có :
AD cạnh chung
góc BAM = góc CAM ( c/m câu a)
AB = AC (gt)
suy ra tam giác ABD = tam giác ACD ( c-g-c)
suy ra : BD = CD ( 2 cạnh tương ứng)
C) hay tam giác BDC cân tại D

Bài 4: a) Xét ABE vàHBE có:
BE chung
ABE= EBH (vì BE là phân giác)
=> ABE=HBE (cạnh huyền- góc nhọn)
b, Vì ABE=HBE(cmt)
=> BA = BH và EA = EH
=> điểm B, E cách đều 2 mút của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c, Vì AC vuông góc BK => EAK = \(90\) độ
EH vuông góc BC => EHC = 90 độ
Xét AEK vàHEC có:
EAK = EHC (= 90độ)(cmt)
AE = EH (cmt)
AEK = HEC (đối đỉnh)
=> AEK HEC (g.c.g)
=> EK = EC (2 cạnh tương ứng)
Xét HEC vuông tại H (vì EHC = 90 độ )
có EH < EC(cạnh huyền lớn hơn cạnh góc vuông)
Mà AE = EH (cmt) => AE < EC

Bạn tự vẽ hình nha!!!
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.
3a.
Xét tam giác ABD vuông tại A và tam giác EBD vuông tại E có:
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (cạnh huyền - góc nhọn)
=> AB = EB (2 cạnh tương ứng) => B thuộc đường trung trực của AE
=> AD = ED (2 cạnh tương ứng) => D thuộc đường trung trực của AE
=> BD là đường trung trực của AE.
3b.
Xét tam giác AFD và tam giác ECD có:
FAD = CED ( = 90 )
AD = ED (tam giác ABD = tam giác EBD)
ADF = EDC (2 góc đối đỉnh)
=> Tam giác ADF = Tam giác EDC (g.c.g)
=> DF = DC (2 cạnh tương ứng)
3c.
Tam giác ADF vuông tại A có:
AD < FD (quan hệ giữa góc và cạnh đối diện trong tam giác vuông)
mà FD = CD (theo câu b)
=> AD < CD.

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

( hình vẽ chỉ mang tính chất minh họa )
a) Xét tam giác ABH và tam giác DBH có :
Góc BAH = Góc BDH ( = 90 độ )
Góc ABH = góc DBH ( gt )
BH chung
=> Tam giác ABH = tam giác DBH ( ch - gn ) - đpcm ( * )
b) Xét tam giác AHE và tam giác DHC có :
Góc EAH = góc CDE ( = 90 độ )
AH = HD ( Theo ( * ) )
Góc AHE = Góc DHC ( đối đỉnh )
=> Tam giác AHE = tam giác DHC ( g.c.g )
=> AE = DC ( 1 )
Từ ( * ) => BA = BD ( 2 )
Từ ( 1 ) và ( 2 ) : BA = BC
=> Tam giác BEC cân tại B - đpcm
c) Ta có góc DHC = góc ABC ( vì cùng phụ với góc BCA ) - đpcm

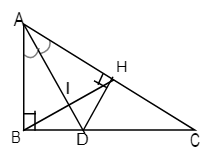
a) Xét ΔABD và ΔAHD có:
∠ABD = ∠AHD = 90 (gt)
Cạnh AD chung
∠BAD = ∠HAD (gt)
⇒ ΔABD = ΔAHD (ch - gn)
b) Xét ΔABC có:
∠B = 90o
⇒ ∠A + ∠C =90o
⇒ ∠C = 90o − ∠A = 90o − 60o = 30o
Vì AD là tia phân giác của ∠A (gt)
⇒ ∠BAD = ∠DAC = ∠A/2 = 60o/2 = 30o
⇒ ∠C = ∠DAC = 30o
⇒ ΔADC cân tại D
⇒ AD = DC
⇒ AH = HC (quan hệ giữa đường xiên và hình chiếu)
c) Xét ΔABD có :
AB < AD (cạnh góc vuông < cạnh huyền)
Mà AD = DC (cmt)
⇒ DC > AB

a) Xét tam giác ABD và tam giác ACD , có :
AD : chung
AB = AC ( gt )
góc ABD = góc ACD ( gt )
=> tam giác ABD = tam giác ACD ( c-g-c )
Vậy tam giác ABD = tam giác ACD ( c-g-c )
b) Xét tam giác ADH và tam giác ADK , có :
AD : chung
góc DAH = góc DAK ( gt )
góc AHD = góc AKD ( = 90o )
=> tam giác ADH = tam giác ADK ( cạnh huyền - góc nhọn )
=> DH = DK ( hai cạnh tương ứng )
=> tam giác DHK cân tại D
Vậy tam giác DHK cân
c) Xét tam giác AHE và tam giác AKF , có :
góc A : chung
AH = AK ( tam giác ADH = tam giác ADK )
góc AHE = góc AKF ( = 90o )
=> tam giác AHE = tam giác AKF ( cạnh góc vuông - góc nhọn kề )
=> AE = AF ( hai cạnh tương ứng )
=> tam giác AEF cân tại A
Xét tam giác AEF cân tại A => góc F = góc E ( tính chất tam giác cân )
=> góc A + góc F + góc E = 180o ( định lý tổng ba góc trong một tam giác )
=> góc F = góc E = \(\dfrac{180^o-\widehat{A}}{2}\) ( 1 )
Xét tam giác ABC cân tại A => góc ABC = góc ACB ( tính chất tam giác cân )
=> góc A + góc ABC + góc ACB = 180o ( định lý tổng ba góc trong một tam giác )
=> góc ABC = góc ACB = \(\dfrac{180^o-\widehat{A}}{2}\) ( 2 )
Từ ( 1 ) và ( 2 ) => góc ABC = góc F mà hai góc ở vị trí đồng vị nên BC // EF ( dấu hiệu nhận biết hai đường thẳng song song )
Vậy BC // EF