Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

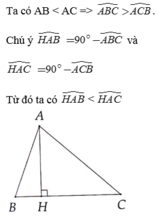
Xét tgiac ABH và ACH đều vuông ở H
Do tổng 3 góc trong 1 tgiac là 180o nên ta có: góc B + HAB = C + HAC = 90o (1)
Xét tgiac ABC có AB < AC => góc C < góc B (2)
(1), (2) => góc HAC > HAB

A B C D E H 1 2 3 4
GT tam giác ABC cân
\(\widehat{A}< 90^o\)
\(BD\perp AC\left(D\in AC\right)\)
\(CE\perp AB\left(E\in AB\right)\)
BD và CE cắt nhau tại H
KL : BD = CD
tam giác BHC cân
AH là đường trung trực của BC
a) Xét tam giác BDC và tam giác CEB có
\(\widehat{BDC}=\widehat{CEB}=90^o\)
BC cạnh chung
\(\widehat{H_1}=\widehat{H_3}\)( 2 góc kề bù )
=> tam giác BDC = tam giác CEB (g-c-g)
=> BD = CE ( 2 cạnh tương ứng )
b) Vì tam giác ABC là tam giác cân
=> \(\widehat{B}=\widehat{C}\)
Vì \(\widehat{B}=\widehat{C}\)
=> tam giác BHC cân
c) Kẻ AH
chép tại https://olm.vn/hoi-dap/detail/79620623509.html :v

hình e tự vẽ nhé
a) Xét tam giác BHA vuông tại H có
góc B + góc HAB = 90 độ ( hai góc phụ nhau)
40 độ + góc HAB = 90 độ
=> góc HAB = 50 độ
mà góc HAB + góc HAC = 90 độ ( tam giác ABC có góc A = 90 độ)
Ta lại có góc HAC + Góc C = 90 độ ( hai góc phụ nhau )
=> góc HAB = góc C = 50 độ

a: Ta có: ΔABC vuông tại A
nên \(\widehat{B}+\widehat{C}=90^0\)
\(\Leftrightarrow\widehat{C}=90^0-40^0=50^0\)

có cần vẽ hình ko bn