Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)a+b+c=9
=>(a+b+c)2=81
=>a2+b2+c2+2ab+2bc+2ca=81
Từ a2+b2+c2=141=>2ab+2bc+2ca=81-141=-60
=>2(ab+bc+ca)=-60=>ab+bc+ca=-30
b)x+y=1
=>(x+y)3=1
=>x3+3x2y+3xy2+y3=1
=>x3+y3+3xy(x+y)=1
=>x3+y3+3xy=1(Do x+y=1)
c)a3-3ab+2c=(x+y)3-3(x+y)(x2+y2)+2(x3+y3)
=x3+3x2y+3xy2+y3-3x3-3y3-3x2y-3xy2+2x3+2y3=0
d)đang tìm hướng giải

Bài 6:
a2+b2=(a+b)2-2ab
<=> 2010 =36-2ab
<=>ab=-987
M=a3+b3
=(a+b)(a2-ab+b2)
=6(a2+987+b^2)
=6(2010+987)
=17982

a, ĐKXĐ: x≠±3
A=\(\left(\dfrac{3-x}{x+3}.\dfrac{x^2+6x+9}{x^2-9}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{3-x}{x+3}.\dfrac{\left(x+3\right)^2}{\left(x+3\right)\left(x-3\right)}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{3-x}{x-3}+\dfrac{x}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{9-x^2}{x^2-9}+\dfrac{x^2-3x}{x^2-9}\right):\dfrac{3x^2}{x+3}\)
A=\(\left(\dfrac{-3}{x+3}\right):\dfrac{3x^2}{x+3}\)
A=\(\dfrac{-1}{x^2}\)
b, Thay x=\(-\dfrac{1}{2}\) (TMĐKXĐ) vào A ta có:
\(\dfrac{-1}{\left(-\dfrac{1}{2}\right)^2}\)=-4
c, A<0 ⇔ \(\dfrac{-1}{x^2}< 0\) ⇔ x2>0 (Đúng với mọi x)
Vậy để A<0 thì x đúng với mọi giá trị (trừ ±3)

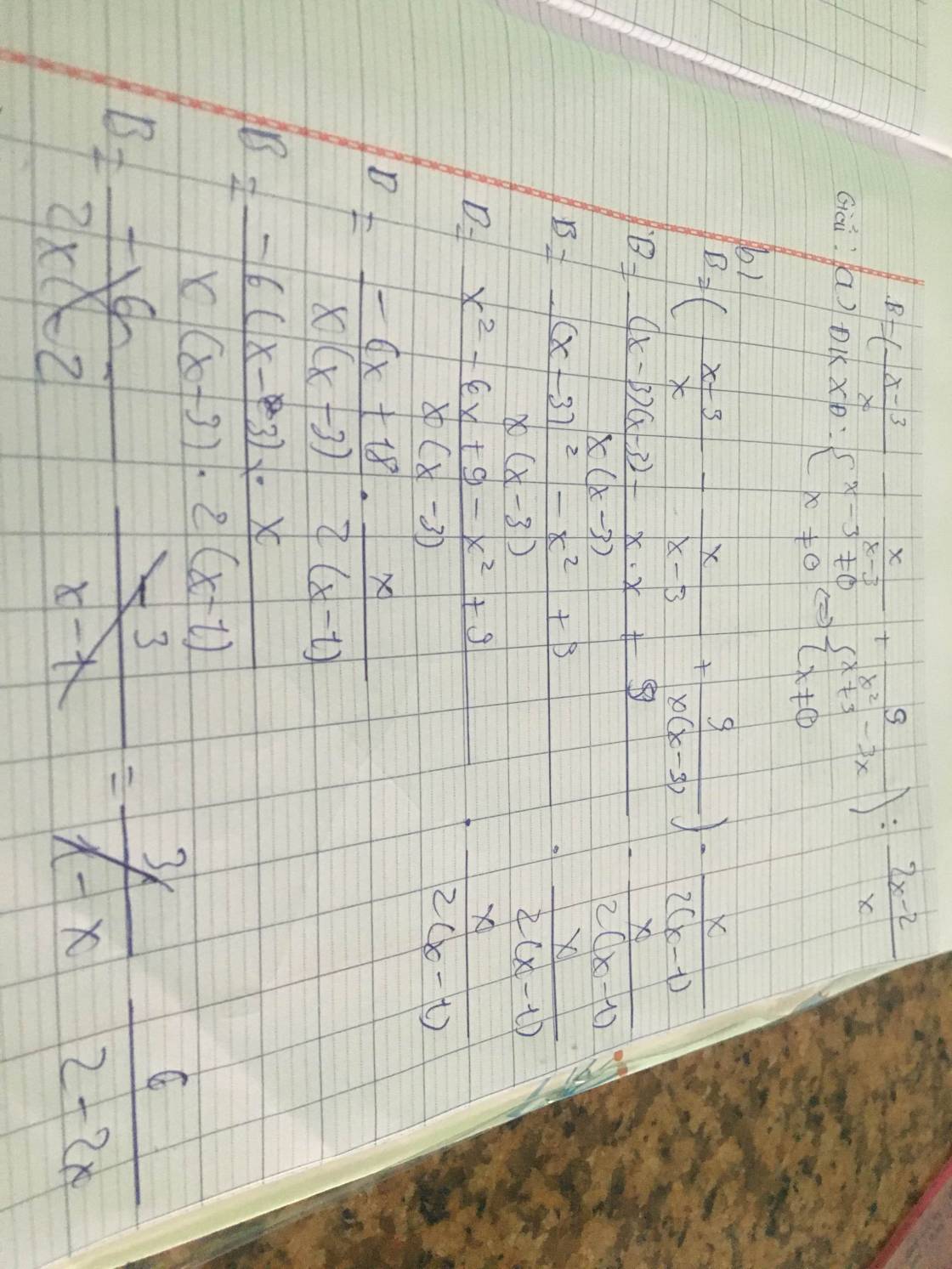 c/
c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.
\(C=a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=a^2-ab+b^2=13-ab\)
Có : \(a^2+2ab+b^2=\left(a+b\right)^2\)
\(\Leftrightarrow13+2ab=1^2\)
\(\Leftrightarrow2ab=-12\)
\(\Leftrightarrow ab=-6\)
\(\Leftrightarrow C=16-\left(-6\right)=13+6=19\)
\(a+b=1\Rightarrow\left(a+b\right)^2=1\)\(\Rightarrow a^2+b^2+2ab=1\)
Mà \(a^2+b^2=13\Rightarrow ab=-6\)
\(\Rightarrow a^3+b^3=\left(a+b\right)\left(a^2+b^2-ab\right)=1.\left[13-\left(-6\right)\right]=19\)