Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
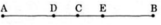
- C là trung điểm AB nên AC = BC.
+ C nằm giữa A và B suy ra CA + CB = AB = 6cm.
+ CA = CB. Kết hợp với CA + CB = 6cm suy ra CA = CB = 3cm.
- Trên tia AB có AD = 2cm < AC = 3cm nên D nằm giữa A và C. Suy ra AD + DC = AC.
- Trên tia BA có BE = 2cm < BC = 3cm nên E nằm giữa C và B. Suy ra BE + EC = BC.
Mà AC = BC nên AD + DC = BE + EC.
Lại có AD = BE nên ta có DC = EC.
- D nằm giữa A và C nên tia CD trùng với tia CA.
E nằm giữa B và C nên tia CE trùng với tia CB.
Tia CA và tia CB đối nhau nên tia CE và tia CD đối nhau. Do đó C nằm giữa D và E.
Kết hợp với DC = EC suy ra C là trung điểm DE.
*Nhận xét:
+ Nếu C là trung điểm của AB thì CA = CB = AB/2.
+ Ngược lại nếu có CA = CB = AB/2 thì suy ra C là trung điểm AB.
Ta có : C là trung điểm AB => AC = BC
mà AD = BE
=> AC - AD = DC = BC - BE = EC
=> DC = EC hay C là trung điểm DE
Ta thấy AD+DC=AC=AB/2=3cm
nên DC=AC-AD=3-2=1cm suy ra D nằm giữa AC(1)
Tương tự: BE+EC=BC=AB/2=3cm
Nên EC=3cm suy ta E nằm giưa BC(2)
Từ (1) và (2) ta có D;C;E thẳng hàng
Vì DC=EC=1 cm suy ra C là trung điểm của DE
Giải:
Vì C là trung điểm của AB nên C nằm giữa A và B và CA=CB= 6:2 = 3(cm).
Trên tia AB có: AD < AC (2<3) nên điểm D nằm giữa A và C, do đó CD=AC-AD=3 – 2 = 1 (cm). Lập luận tương tự ta được điểm E nằm giữa B và C và CE=1cm. Ta thấy điểm C nằm giữa D và E.
Mặt khác có CD=CE(=1cm) nên C là trung điểm của D và E.
Vì \(C\) là trung điểm của \(AB\)
⇒ \(AC=CB=\dfrac{AB}{2}=3\left(cm\right)\)
\(CD=AC-AD=3-2=1\left(cm\right)\)
\(CE=CB-EB=3-2=1\left(cm\right)\)
Vì \(CD=CE\)
mà \(C,D,E\) thẳng hàng
⇒ \(C\) là trung điểm của \(DE\)