Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi \(3n+1\in B\left(63\right)\) hoặc \(3n+1\inƯ\left(63\right)\)
\(A=\frac{63+1}{3n}\left(n\in N\right)\)
Ta rút gọn được :
+\(3n+1\in B\left(63\right)\)
+\(3n+1\inƯ\left(63\right)\)

Có đầy câu hỏi tương tự đáy bạn lên các câu hỏi đó mà xem

a: \(A=\dfrac{a^3+a^2+a^2+a-a-1}{\left(a+1\right)\left(a^2-a+1\right)+2a\left(a+1\right)}\)
\(=\dfrac{\left(a+1\right)\left(a^2+a-1\right)}{\left(a+1\right)\left(a^2+a+1\right)}=\dfrac{a^2+a-1}{a^2+a+1}\)
b: Nếu a là số nguyên âm thì a<0
Vì a2+a=a(a+1) chia hết cho 2 nên \(a^2+a-1;a^2+a+1\) là hai số tự nhiên lẻ liên tiếp
hay A là phân số tối giản

Đáp án A
Dễ dàng suy ra:
A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c , a , b , c > 0
vì d M ; O B C = d M ; O y z = x M = 1 , tương tự ta có được M 1 ; 2 ; 3
M ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 1.2.3 a . b . c 3 ⇔ a b c 6 = V O . A B C ≥ 27
Dấu bằng xảy ra khi:
1 a = 2 b = 3 c = 1 3 ⇒ a = 3 ; b = 6 ; c = 9 ⇒ a + b + c = 18

Chọn đáp án D
Giả sử mặt phẳng (P) có vectơ pháp tuyến là n ⇀ = a ; b ; c a 2 + b 2 + c 2 ≠ 0 .
Khi đó phương trình mặt phẳng (P) có dạng a x + b y + c z + d = 0 .
Do M 0 ; 0 ; 1 ∈ P nên c + d = 0 ⇔ d = - c
Do N 0 ; 3 ; 1 ∈ P nên 3 b + c + d = 0 ⇔ b = 0
Khi đó P : a x + c z - c = 0
Từ giả thiết ta có d B ; P = 2 d A ; P
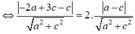
⇔ - 2 a + 2 c a 2 + c 2 = 2 a - c a 2 + c 2 (luôn đúng). Vậy có vô số mặt phẳng (P) thỏa mãn.

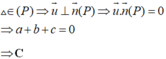
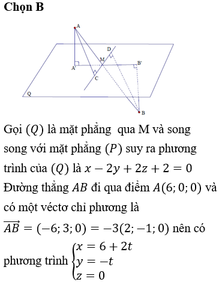

các bạn giúp mình với mình cần gấp lắm


có bạn nào làm được ko