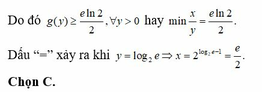Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Ta có: 2 x + 1 4 y 2 x + y ≥ 2 + 1 2 2 (Bất đẳng thức Bunhia Scopky).
(ngoài ra các em có thể thế và xét hàm).
Do đó P ≥ 5.
Đáp án C
Áp dụng bất đẳng thức Bunhiacopxki,
ta có 2 x + 1 4 y 2 x + y ≥ 2 + 1 2 2 ⇒ P ≥ 5
Chọn đáp án B
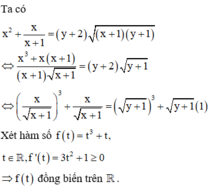
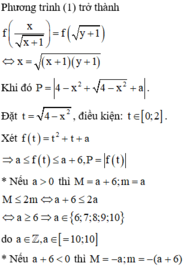
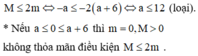
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
Đáp án A
Ta có: 5 4 2 x − 5 y ≥ 2 5 6 x − 2 y
⇔ 5 4 2 x − 5 y ≥ 5 2 2 x − 6 y ⇔ 5 2 4 x − 10 y ≥ 5 2 2 x − 6 y
⇔ 4 x − 10 y ≥ 2 x − 6 y ⇔ 2 x ≥ 4 y ⇔ x y ≥ 2 .
Vậy giá trị nhỏ nhất của x y là 2.
