VT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
1 tháng 1 2022
a thuộc N nên a có dạng 5k,5k+1,5k+2,5k+3,5k+4
với a=5k thì a^2 và a chia hết cho 5 mà 2021 ko chia hết nên tổng ko chia hết
với a=5k+1 =>a2+a+2021=(5k+1)2+5k+1+2021=25k2+15k+2023 không chia hết cho 5
bạn làm tương tự với mấy cây còn lại, ko đc thì nói nhé
chúc bạn học tốt
NNBC-1/1/2022
TV
1
TN
2
28 tháng 12 2021
=1811.39267016hoac 1811du75
chuc ban hoc tot
nho k cho mk nho
28 tháng 12 2021
số chia hết cho 5 có tận cùng là 5 hoặc 0
mà trong tổng có 1 thừa số là 2021 có tận cùng là 1 nên cả tổng sẽ không chia hết cho 5
KT
12 tháng 8 2018
a) \(\overline{aaaaaa}=a.111111=a.3.37037\) \(⋮\)\(37037\)
b) Nhận thấy các hạng tử trong B đều chia hết cho 3 => B chia hết cho 3
\(B=3+3^3+3^5+3^7+...+3^{2017}+3^{2019}+3^{2021}\)
\(=\left(3+3^3+3^5\right)+\left(3^7+3^9+3^{11}\right)+....+\left(3^{2017}+3^{2019}+3^{2021}\right)\)
\(=3\left(1+3^2+3^4\right)+3^7\left(1+3^2+3^4\right)+...+3^{2017}\left(1+3^2+3^4\right)\)
\(=\left(1+3^2+3^4\right)\left(3+3^7+...+3^{2017}\right)\)
\(=91\left(3+3^7+....+3^{2017}\right)\)\(⋮\)\(91\)
mà (3;91) = 1
=> B chia hết cho 273
LT
12 tháng 8 2018
B chia hết cho 273
Còn câu a thì mình không biết nhé, xin lỗi bạn.
HP
1
14 tháng 2 2019
Phần a có 2 cách nha bạn:
-C1:Ta thấy tổng các chữ số của ababab là :a+b+a+b+a+b =3a+3b=3x(a+b) chia hết cho 3
Vậy ababab chia hết cho 3
-C2:ta có :ababab=a x100000+b x10000+a x1000+b x100+a x10+b
=a x101010+b x10101
=3x(a x33670+b x3367) chia hết cho 3
Vậy ababab chia hết cho 3
NM
Nguyễn Minh Quang
Giáo viên
13 tháng 10 2021
ta có a+2021 và a+2020 là hai số tự nhiên liên tiếp
nên chắc chắc có 1 số chẵn trong hai số đó
vậy tích (a+2021)(a+2020) là số chẵn, hay là bội của 2
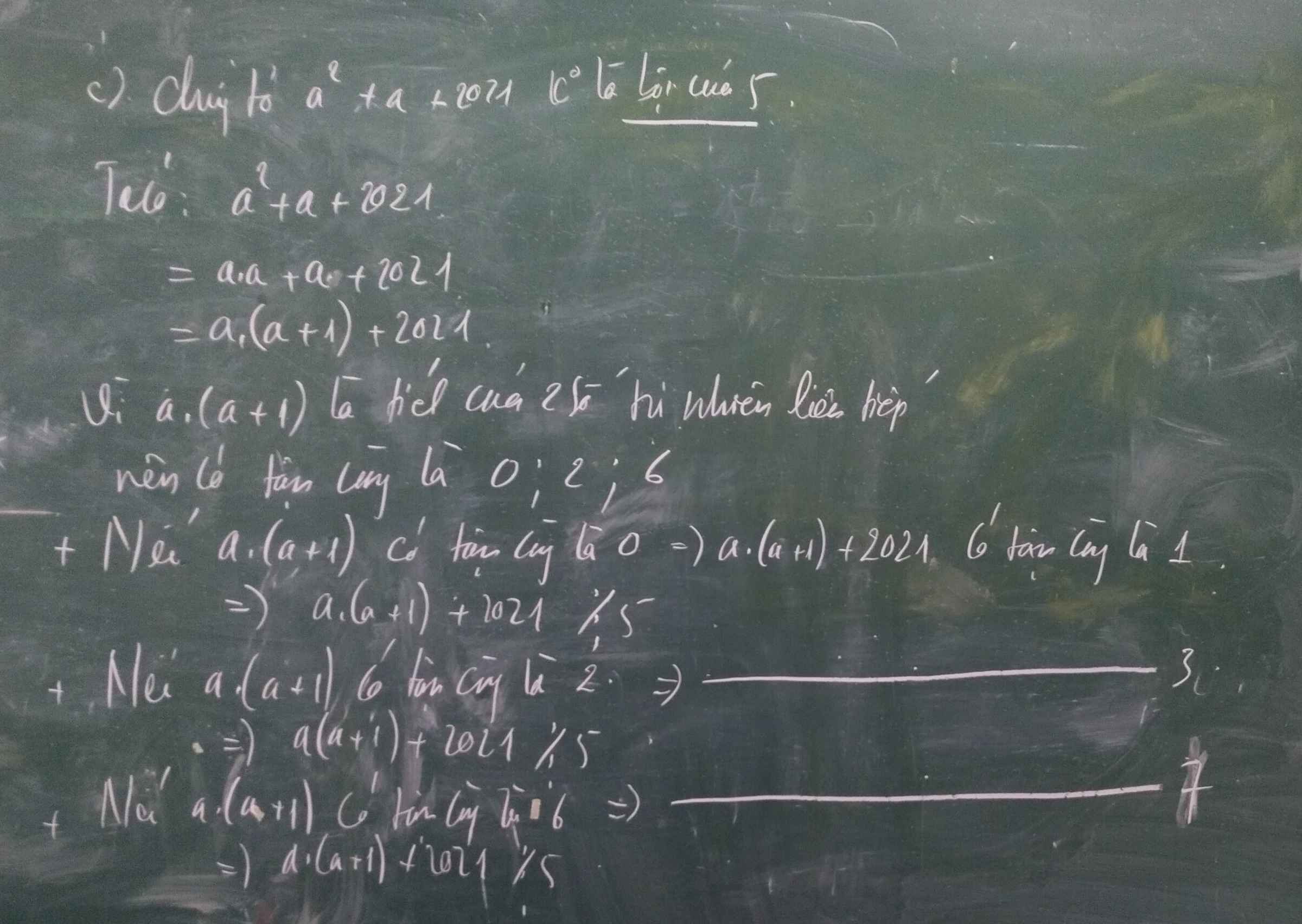
\(a^2+a+2021=a\left(a+1\right)+2021\)
a và (a+1) là hai số TN liên tiếp => tích a(a+1) có chữ số tận cùng = {0;2;6}
=> a(a+1)+2021 có chữ số tận cùng = {1;3;7}\(\Rightarrow a^2+a+2021\) không chia hết cho 5 nên nó không phải bội của 5