Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

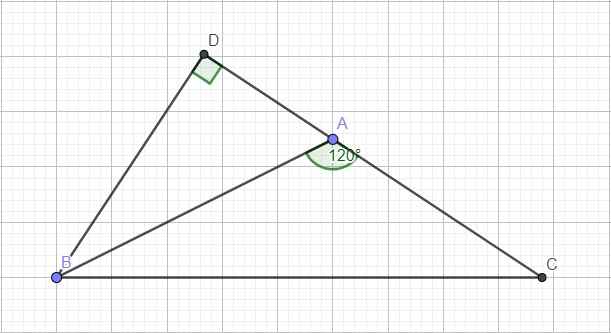
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)

Cauchy ở mẫu \(a^2+bc\ge2a\sqrt{bc}\)
Vậy vế trái \(\le\frac{1}{2a\sqrt{bc}}+\frac{1}{2b\sqrt{ca}}+\frac{1}{2c\sqrt{ab}}=\frac{\sqrt{ab}+\sqrt{bc}+\sqrt{ca}}{2abc}\)
Và lượng trên tử bé hơn bằng \(ab+bc+ca\)

Ta có:
\(a< b+c\)
\(\Leftrightarrow2a< a+b+c=2\)
\(\Leftrightarrow a< 1\)
Tương tự ta cũng có:
\(\hept{\begin{cases}b< 1\\c< 1\end{cases}}\)
\(\Rightarrow\left(1-a\right)\left(1-b\right)\left(1-c\right)>0\)
\(\Leftrightarrow-abc+ab+bc+ca-a-b-c+1>0\)
\(\Leftrightarrow abc< \left(ab+bc+ca\right)-1\)
\(\Leftrightarrow2abc< 2\left(ab+bc+ca\right)-2\)
\(\Leftrightarrow a^2+b^2+c^2+2abc< a^2+b^2+c^2+2\left(ab+bc+ca\right)-2\)
\(\Leftrightarrow a^2+b^2+c^2+2abc< \left(a+b+c\right)^2+2=4-2=2\)

Sửa đề: 1+a^2;1+b^2;1+c^2
\(\dfrac{a}{\sqrt{1+a^2}}=\dfrac{a}{\sqrt{a^2+ab+c+ac}}=\sqrt{\dfrac{a}{a+b}\cdot\dfrac{a}{a+c}}< =\dfrac{1}{2}\left(\dfrac{a}{a+b}+\dfrac{a}{a+c}\right)\)
\(\dfrac{b}{\sqrt{1+b^2}}< =\dfrac{1}{2}\left(\dfrac{b}{b+c}+\dfrac{b}{b+a}\right)\)
\(\dfrac{c}{\sqrt{1+c^2}}< =\dfrac{1}{2}\left(\dfrac{c}{c+a}+\dfrac{c}{a+b}\right)\)
=>\(A< =\dfrac{1}{2}\left(\dfrac{a+b}{a+b}+\dfrac{b+c}{b+c}+\dfrac{c+a}{c+a}\right)=\dfrac{3}{2}\)

Do mình chưa học lớp 9, nên không thể giải bài của bạn. Mình có tìm trên mạng và đã tìm được lời giải này cho bạn. Thực mình không hiểu đâu, mong bạn thông cảm.
Nguồn : http://diendantoanhoc.net/topic/81625-sinfraca2leq-fraca2sqrtbc/
Mình sử dụng công thức \(S=\frac{AB.AC.Sin_A}{2}.\).
Vẽ tia phân giác AD của góc A.Đặt \(l=AD\)
\(S_{ABC}=S_{ABD}+S_{ACD}\)
\(=\frac{cl.Sin_{\frac{A}{2}}}{2}+\frac{bl.Sin_{\frac{A}{2}}}{2}\)
\(=\frac{l.Sin_{\frac{A}{2}}\left(b+c\right)}{2}\)
Mặt khác \(S_{ABC}\le\frac{al}{2}\)
\(\Leftrightarrow Sin_{\frac{A}{2}}\le\frac{a}{b+c}\left(\le\frac{a}{2\sqrt{bc}}\right)\) :)