Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Từ a + 5 < b + 5
=> a + 5 + (-5) < b + 5 + (-5) (cộng hai vế với -5)
=> a < b
a)từ a+5<b+5 ta cộng -5 vào 2 vế được a<b
b)từ -3a>-3b ta nhân 2 vế với -1/3 (tức là chia cả 2 vế cho -3) và -3a . -1/3< -3b . -1/3 sẽ được a<b

Ta luôn có
\(x^2+2xy+y^2=\left(x+y\right)^2\) ( hẳng đẳng thức )
\(\Rightarrow A=\left(2a-3b\right)^2+2\left(2a-3b\right)\left(3a-2b\right)+\left(2b-3a\right)^2\)
\(=\left(2a-3b\right)^2+2\left(2a-3b\right)\left(3a-2b\right)+\left(3a-2b\right)^2\)
\(=\left[\left(2a-3b\right)+\left(3a-2b\right)\right]^2\)
\(=\left(2a-3b-2b+3a\right)^2\)
\(=\left(a-b\right)^2\)
\(=10^2\)
\(=100\)

Từ \(a-2b=5\Rightarrow a=5+2b\) thay vào P ta có:
\(P=\frac{3\left(2b+5\right)-2b}{2\left(2b+5\right)+5}+\frac{3b-\left(2b+5\right)}{b-5}\)\(=\frac{6b+15-2b}{4b+10+5}+\frac{3b-2b+5}{b-5}\)
\(=\frac{4b+15}{4b+15}+\frac{b-5}{b-5}=1+1=2\)

Lấy ví dụ rồi đưa ra kết quả:
A = 1
B = 0
3 - 2a = 3 - 21 = -18
5 - 2b = 5 - 20 = -15
Mà -18 < -15
Nên: 3 - 2a < 5 - 2b

Ap dung bdt \(\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right).\left(x,y>0\right)\) lien tiep la duoc
Chuc bn thanh cong
svác-xơ ngược dấu.
\(\frac{16}{2a+3b+3c}=\frac{16}{\left(a+b\right)+\left(c+b\right)+\left(b+c\right)+\left(a+c\right)}\le\frac{1}{a+b}+\frac{2}{c+b}+\frac{1}{c+a}\)
Tương tự
\(\frac{16}{2b+3c+3a}\le\frac{1}{a+b}+\frac{1}{b+c}+\frac{2}{c+a}\)
\(\frac{16}{2c+3a+3b}\le\frac{2}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\)
Cộng lại ta được:
\(16VT\le4\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\)
\(\Rightarrow VT\le\frac{1}{4}\left(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{c+a}\right)\left(đpcm\right)\)

\(P=\frac{a^3}{2a+3b}+\frac{b^3}{3a+2b}=\frac{a^4}{2a^2+3ab}+\frac{b^4}{3ab+2b^2}\)
\(P\ge\frac{\left(a^2+b^2\right)^2}{2\left(a^2+b^2\right)+6ab}\ge\frac{\left(a^2+b^2\right)^2}{2\left(a^2+b^2\right)+3\left(a^2+b^2\right)}=\frac{a^2+b^2}{5}=\frac{2}{5}\)
Dấu "=" xảy ra khi \(a=b=1\)
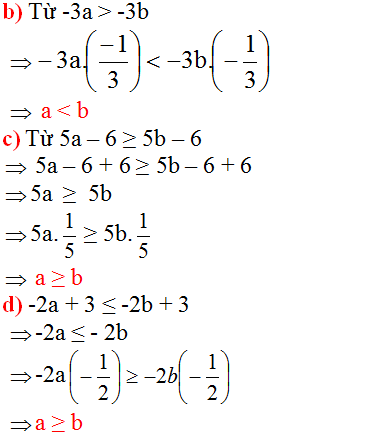
a) 3a + 5 > 3b + 5; b) 2a - 3 > 2b - 4