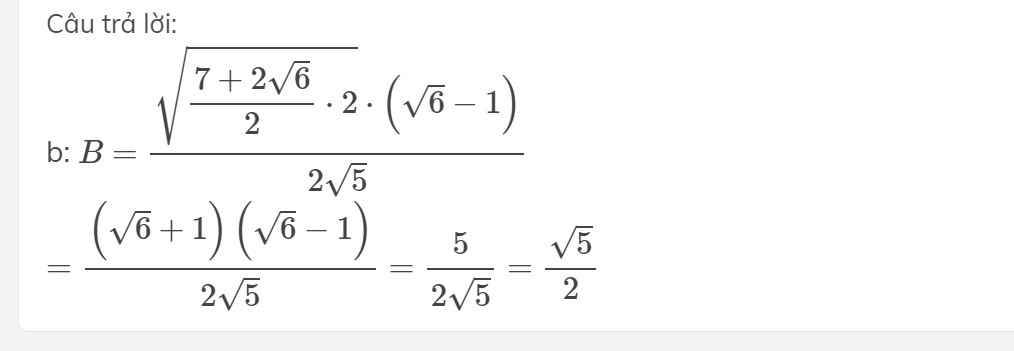Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có \(\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2=a+b+c+2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\Leftrightarrow7^2=23+2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\Leftrightarrow\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=13\)
Ta lại có \(\sqrt{a}+\sqrt{b}+\sqrt{c}=7\Leftrightarrow\sqrt{c}-6=-\sqrt{a}-\sqrt{b}+1\Leftrightarrow\sqrt{ab}+\sqrt{c}-6=\sqrt{ab}-\sqrt{a}-\sqrt{b}+1=\sqrt{a}\left(\sqrt{b}-1\right)-\left(\sqrt{b}-1\right)=\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)\)
Chứng minh tương tự:
\(\sqrt{bc}+\sqrt{a}-6=\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)\)
\(\sqrt{ac}+\sqrt{b}-6=\left(\sqrt{a}-1\right)\left(\sqrt{c}-1\right)\)
Vậy A=\(\dfrac{1}{\sqrt{ab}+\sqrt{c}-6}+\dfrac{1}{\sqrt{bc}+\sqrt{a}-6}+\dfrac{1}{\sqrt{ca}+\sqrt{b}-6}=\dfrac{1}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)}+\dfrac{1}{\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)}+\dfrac{1}{\left(\sqrt{c}-1\right)\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{c}-1+\sqrt{a}-1+\sqrt{b}-1}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)}=\dfrac{\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)-3}{\sqrt{abc}+\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)-\left(\sqrt{ab}+\sqrt{ac}+\sqrt{bc}\right)}=\dfrac{7-3}{3+7-13-1}=-1\)
Câu hỏi của hoàng thị huyền trang - Toán lớp 9 - Học toán với OnlineMath
Em tham khảo nhé!
Từ giả thiết: \(\sqrt{a}+\sqrt{b}+\sqrt{c}=7\Leftrightarrow\sqrt{c}=7-\sqrt{a}-\sqrt{b}\)
Xét hạng tử: \(\frac{1}{\sqrt{ab}+\sqrt{c}-6}=\frac{1}{\sqrt{ab}+7-\sqrt{a}-\sqrt{b}-6}=\frac{1}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)}\)
Từ đó: \(N=\frac{1}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)}+\frac{1}{\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)}+\frac{1}{\left(\sqrt{c}-1\right)\left(\sqrt{a}-1\right)}\)
\(=\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}-3}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)}=\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}-3}{\sqrt{abc}-\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)+\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)-1}\)
\(=\frac{7-3}{3-\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)+7-1}=\frac{4}{9-\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)}\)
Mặt khác: \(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\frac{\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2-\left(a+b+c\right)}{2}=13\)
Suy ra: \(N=\frac{4}{9-13}=-1\). Kết luận: N = -1.
Từ giả thiết: \sqrt{a}+\sqrt{b}+\sqrt{c}=7\Leftrightarrow\sqrt{c}=7-\sqrt{a}-\sqrt{b}a+b+c=7⇔c=7−a−b
Xét hạng tử: \frac{1}{\sqrt{ab}+\sqrt{c}-6}=\frac{1}{\sqrt{ab}+7-\sqrt{a}-\sqrt{b}-6}=\frac{1}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)}ab+c−61=ab+7−a−b−61=(a−1)(b−1)1
Từ đó: N=\frac{1}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)}+\frac{1}{\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)}+\frac{1}{\left(\sqrt{c}-1\right)\left(\sqrt{a}-1\right)}N=(a−1)(b−1)1+(b−1)(c−1)1+(c−1)(a−1)1
=\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}-3}{\left(\sqrt{a}-1\right)\left(\sqrt{b}-1\right)\left(\sqrt{c}-1\right)}=\frac{\sqrt{a}+\sqrt{b}+\sqrt{c}-3}{\sqrt{abc}-\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)+\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)-1}=(a−1)(b−1)(c−1)a+b+c−3=abc−(ab+bc+ca)+(a+b+c)−1a+b+c−3
=\frac{7-3}{3-\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)+7-1}=\frac{4}{9-\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)}=3−(ab+bc+ca)+7−17−3=9−(ab+bc+ca)4
Mặt khác: \sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\frac{\left(\sqrt{a}+\sqrt{b}+\sqrt{c}\right)^2-\left(a+b+c\right)}{2}=13ab+bc+ca=2(a+b+c)2−(a+b+c)=13
Suy ra: N=\frac{4}{9-13}=-1N=9−134=−1. Kết luận: N = -1.
a) \(A=\dfrac{2}{\sqrt{3}+1}+\dfrac{6}{\sqrt{3}-1}+1\)
\(=\dfrac{3\left(\sqrt{3}-1\right)}{2}+\dfrac{6\left(\sqrt{3}+1\right)}{2}+\dfrac{2}{2}\)
\(=\dfrac{3\left(\sqrt{3}-1\right)+6\left(\sqrt{3}+1\right)+2}{2}\)
\(=\dfrac{3\sqrt{3}-3+6\sqrt{3}+6+2}{2}\)
\(=\dfrac{9\sqrt{3}+5}{2}\)
a) \(A=\dfrac{2}{\sqrt{3}+1}+\dfrac{6}{\sqrt{3}-1}+1\)
\(=\dfrac{2\left(\sqrt{3}-1\right)}{2}+\dfrac{6\left(\sqrt{3}+1\right)}{2}+\dfrac{2}{2}\)
\(=\dfrac{2\left(\sqrt{3}-1\right)+6\left(\sqrt{3}+1\right)+2}{2}\)
\(=\dfrac{2\sqrt{3}-2+6\sqrt{3}+6+2}{2}\)
\(=\dfrac{8\sqrt{3}+6}{2}\)
\(=\dfrac{2\left(4\sqrt{3}+3\right)}{2}\)
\(=4\sqrt{3}+3\)
b: \(B=\dfrac{\sqrt{\dfrac{7+2\sqrt{6}}{2}\cdot2}\cdot\left(\sqrt{6}-1\right)}{2\sqrt{5}}\)
\(=\dfrac{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}{2\sqrt{5}}=\dfrac{5}{2\sqrt{5}}=\dfrac{\sqrt{5}}{2}\)
\(\sqrt{\dfrac{ab}{c+ab}}=\sqrt{\dfrac{ab}{c\left(a+b+c\right)+ab}}=\sqrt{\dfrac{ab}{\left(a+c\right)\left(b+c\right)}}\le\dfrac{1}{2}\left(\dfrac{a}{a+c}+\dfrac{b}{b+c}\right)\)
Tương tự: \(\sqrt{\dfrac{bc}{a+bc}}\le\dfrac{1}{2}\left(\dfrac{b}{a+b}+\dfrac{c}{a+c}\right)\) ; \(\sqrt{\dfrac{ca}{b+ca}}\le\dfrac{1}{2}\left(\dfrac{a}{a+b}+\dfrac{c}{b+c}\right)\)
Cộng vế với vế:
\(P\le\dfrac{1}{2}\left(\dfrac{a}{a+c}+\dfrac{c}{a+c}+\dfrac{b}{b+c}+\dfrac{c}{b+c}+\dfrac{b}{a+b}+\dfrac{a}{a+b}\right)=\dfrac{3}{2}\)
Dấu "=" xảy ra khi \(a=b=c=\dfrac{1}{3}\)
Cho a, b, c, d là các chữ số thỏa mãn: ab+ca=da ab-ca=a Tìm giá trị của d.