Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
a) Để xác định tập hợp \(A = (1;3) \cup [ - 2;2]\), ta vẽ sơ đồ sau đây:
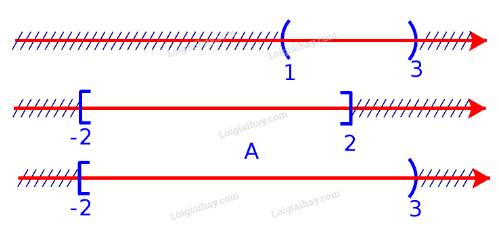
Từ sơ đồ, ta thấy \(A = [ - 2;3)\)
b) Để xác định tập hợp \(B = ( - \infty ;1) \cap [0;\pi ]\), ta vẽ sơ đồ sau đây:
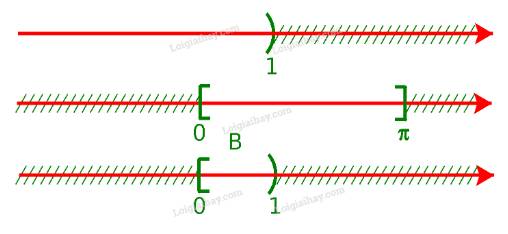
Từ sơ đồ, ta thấy \(B = [0;1)\)
c) Để xác định tập hợp \(C = [\frac{1}{2};3){\rm{\backslash }}(1; + \infty )\), ta vẽ sơ đồ sau đây:
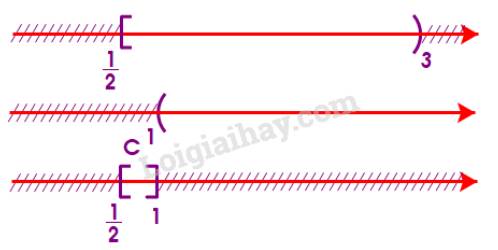
Từ sơ đồ, ta thấy \(C = [\frac{1}{2};1]\)
d) Để xác định tập hợp \(D = {C_\mathbb{R}}[ - 1; + \infty )\), ta vẽ sơ đồ sau đây:
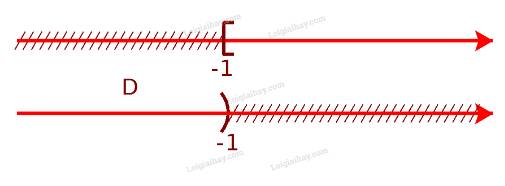
Từ sơ đồ, ta thấy \(D = ( - \infty ; - 1)\)

Tham khảo:
+) \(A \cap B = [0;3] \cap (2; + \infty ) = (2;3]\)

+) \(A \cup B = [0;3] \cup (2; + \infty ) = [0; + \infty )\)

+) \(A\,{\rm{\backslash }}\,B = [0;3]\,{\rm{\backslash }}\,(2; + \infty ) = [0;2]\)

+) \(B\,{\rm{\backslash }}\,A = (2; + \infty )\,{\rm{\backslash }}\,[0;3] = (3; + \infty )\)

+) \(\mathbb{R}\,{\rm{\backslash }}\,B = \mathbb{R}\,{\rm{\backslash }}\,(2; + \infty ) = ( - \infty ;2]\)


Tham khảo:
a) Ta có:

Giao của hai tập hợp là \(( - 4;1] \cap [0;3) = \left[ {0;1} \right]\)
b) Ta có:
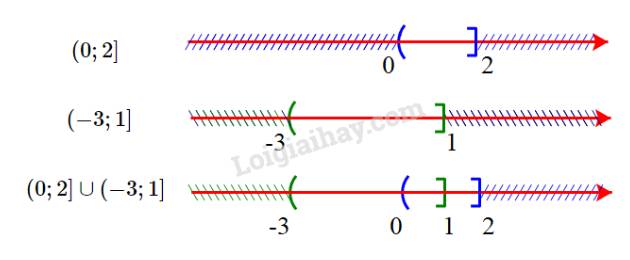
Hợp của hai tập hợp là \((0;2] \cup ( - 3;1] = ( - 3;2]\)
c) Ta có:
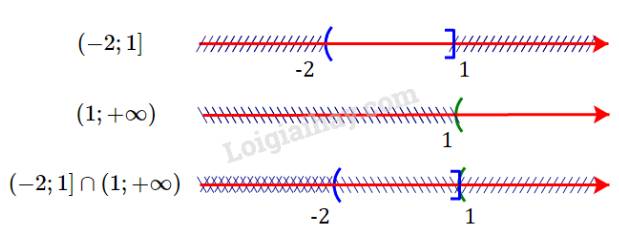
Giao của hai tập hợp là \(( - 2;1] \cap (1;+ \infty )= \emptyset\)
d) Ta có:

Phần bù của tập hợp \(( - \infty ;3]\) trong \(\mathbb{R}\) là \(\mathbb{R}{\rm{\backslash }}( - \infty ;3] = (3; + \infty )\)

Tham khảo:
a) Đặt \(A = [ - 3;7] \cap (2;5)\)
Tập hợp A là khoảng (2; 5) và được biểu diễn là:
a) Đặt \(A = [ - 3;7] \cap (2;5)\)
Tập hợp A là khoảng (2; 5) và được biểu diễn là:

b) Đặt \(B = ( - \infty ;0] \cup ( - 1;2)\)
Tập hợp B là khoảng \(( - \infty ;2)\) và được biểu diễn là:

c) Đặt \(C = \mathbb{R}\,{\rm{\backslash }}\,( - \infty ;3)\)
Tập hợp C là nửa khoảng \([3; + \infty )\) và được biểu diễn là:

d) Đặt \(D = ( - 3;2)\,{\rm{\backslash }}\,[1;3)\)
Bỏ đi các điểm thuộc [1;3) trong khoảng (-3;2)
Tập hợp D là khoảng \(( - 3;1)\) và được biểu diễn là:

b) Đặt \(B = ( - \infty ;0] \cup ( - 1;2)\)
Tập hợp B là khoảng \(( - \infty ;2)\) và được biểu diễn là:

c) Đặt \(C = \mathbb{R}\,{\rm{\backslash }}\,( - \infty ;3)\)
Tập hợp C là nửa khoảng \([3; + \infty )\) và được biểu diễn là:

d) Đặt \(D = ( - 3;2)\,{\rm{\backslash }}\,[1;3)\)
Bỏ đi các điểm thuộc [1;3) trong khoảng (-3;2)
Tập hợp D là khoảng \(( - 3;1)\) và được biểu diễn là:


\(E = \{ x \in \mathbb{N}|x < 8\} = \{ 0;1;2;3;4;5;6;7\} \)
a) Ta có: \(A\backslash B = \left\{ {0;1;2} \right\}\), \(B\backslash A = \left\{ 5 \right\},\)\((A\backslash B) \cap {\rm{(}}B\backslash A) = \emptyset \)
b) Ta có: \(A \cap B = \{ 3;4\} ,\;{C_E}(A \cap B) = \{ 0;1;2;5;6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cap ({C_E}B) = \{ 6;7\} \)
c) Ta có: \(A \cup B = \{ 0;1;2;3;4;5\} ,\;{C_E}(A \cup B) = \{ 6;7\} \)
\({C_E}A = \{ 5;6;7\} ,\;{C_E}B = \{ 0;1;2;6;7\} \Rightarrow ({C_E}A) \cup ({C_E}B) = \{ 0;1;2;5;6;7\} \)

\(A = \left\{ {0;1;2;3;4;5;6} \right\}\)
\(\,B = \left\{ {1;2;3;6;7;8} \right\}\)
Vậy
\(A \cap B = \left\{ {1;2;3;6} \right\}\)
\(A \cup B = \left\{ {0;1;2;3;4;5;6;7;8} \right\} = \left\{ {x \in \mathbb{N}|\;x < 9} \right\}\)
\(A\;{\rm{\backslash }}\;B = \left\{ {0;4;5} \right\}\)

Tham khảo:
a) Để xác định tập hợp \(A = ( - \infty ;0] \cup [ - \pi ;\pi ]\), ta vẽ sơ đồ sau đây:
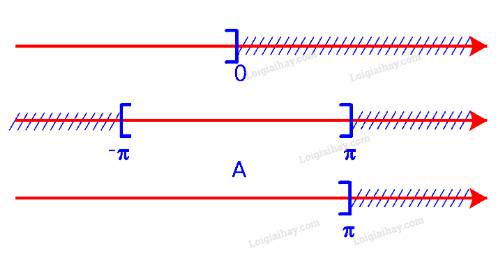
Từ sơ đồ, ta thấy \(A = ( - \infty ;\pi ]\)
b) Để xác định tập hợp \(B = [ - 3,5;2] \cap ( - 2;3,5)\), ta vẽ sơ đồ sau đây:
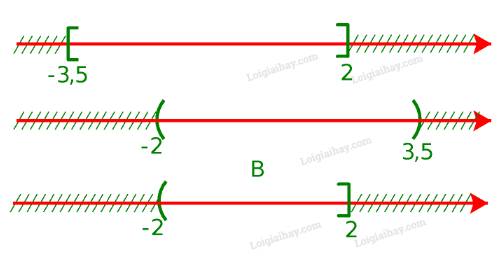
Từ sơ đồ, ta thấy \(B = ( - 2;2]\)
c) Để xác định tập hợp \(C = ( - \infty ;\sqrt 2 ] \cap [1; + \infty )\), ta vẽ sơ đồ sau đây:
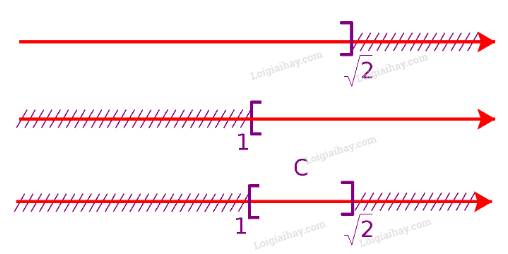
Từ sơ đồ, ta thấy \(C = [1;\sqrt 2 ]\)
d) Để xác định tập hợp \(D = ( - \infty ;\sqrt 2 ]{\rm{\backslash }}[1; + \infty )\), ta vẽ sơ đồ sau đây:
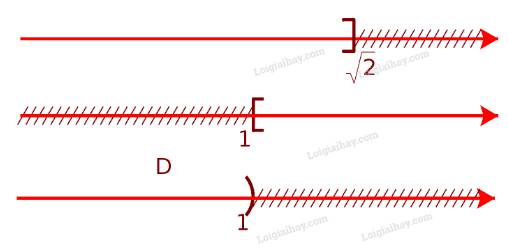
Từ sơ đồ, ta thấy \(D = ( - \infty ;1)\)

Tham khảo:
a) Ta có:
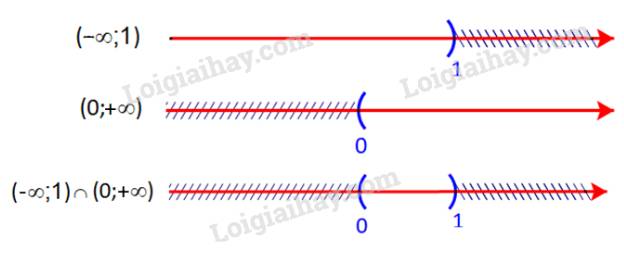
Giao của hai tập hợp là \(( - \infty ;1) \cap (0; + \infty ) = (0;1)\)
b) Ta có:

Hợp của hai tập hợp là \((4;7] \cup ( - 1;5) = ( - 1;7]\)
c) Ta có:
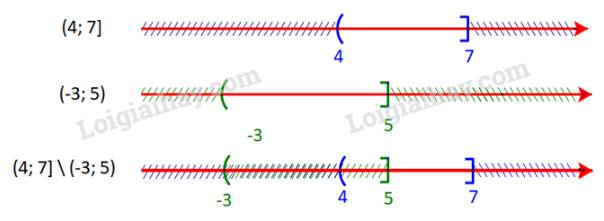
Hiệu của tập hợp \((4;7]\) và tập hợp \(( - 3;5]\) là \((4;7]\;{\rm{\backslash }}\;( - 3;5] = (5;7]\)

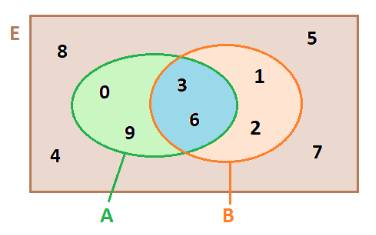
\(E = \{ x \in \mathbb{N}|x < 10\} = \{ 0;1;2;3;4;5;6;7;8;9\} \)
\(A = \{ x \in E|x\) là bội của 3\(\} \)\( = \{ 0;3;6;9\} \)
\(B = \{ x \in E|x\) là ước của 6\(\} \)\( = \{1;2;3;6\} \)
Ta có: \(A\backslash B = \left\{ {0;9} \right\}\), \(B\backslash A = \left\{ {1;2} \right\}\)
\({C_E}A = \{ 1;2;4;5;7;8\} ,\;{C_E}B = \{ 0;4;5;7;8;9\} \)
\(A \cap B = \{ 3;6\} \Rightarrow {C_E}(A \cap B) = {C_E}B = \{0;1;2;4;5;7;8;9\} \)
\(A \cup B = \{ 0;1;2;3;6;9\} \Rightarrow {C_E}(A \cup B) = {C_E}A = \{ 4;5;7;8\} \)
Giao của hai tập hợp là \([ - 2;3] \cap (1; + \infty ) = (1;3]\)
Hiệu của \(B \backslash A \) là \( (1; + \infty ) \backslash [ - 2;3] = (3; + \infty )\)
Phần bù của B trong \(\mathbb{R}\) là: \({C_\mathbb{R}}\;B = \mathbb{R}{\rm{\backslash }}\;(1; + \infty ) = ( - \infty ;1]\)