K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
13 tháng 4 2017
a) D nằm trên trục Ox nên D có tọa độ D(x ; 0)
Khi đó :
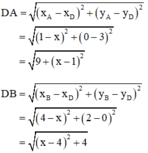
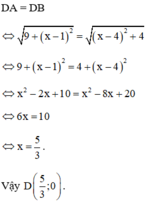
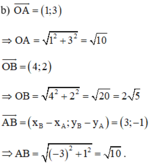
Vậy chu vi tam giác OAB là P = AO + BO + AB = √10 + 2√5 + √10 = 2√5 + 2√10
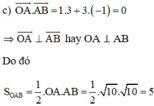

9 tháng 2 2023
a: vecto AB=(2;2)=(1;1)
=>VTPT là (-1;1)
Phương trình tham số AB là: \(\left\{{}\begin{matrix}x=-1+t\\y=0+t=t\end{matrix}\right.\)
Phương trình tổng quát của AB là:
-1(x+1)+1(y-0)=0
=>-x-1+y=0
=>x-y+1=0
b: vecto BC=(2;0)
Vì AH vuông góc BC
nên AH nhận vecto BC làm vtpt và đi qua A
=>AH: 2(x+1)+0(y-0)=0
=>2x+2=0
=>x=-1
c: Tọa độ M la:
x=(-1+3)/2=2/2=1 và y=(0+2)/2=1
B(1;2); M(1;1)
vecto BM=(0;-1)
=>VTPT là (1;0)
Phương trình BM là:
1(x-1)+0(y-2)=0
=>x-1=0
=>x=1