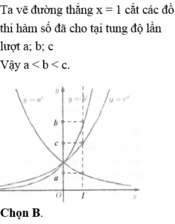
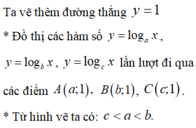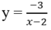Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

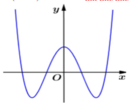
\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)

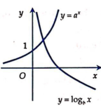
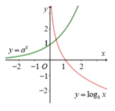
Do y = ax và y = bx là hai hàm đồng biến nên a > 1; b > 1.
Do y = cx nghịch biến nên c < 1. Vậy c bé nhất.
Mặt khác: Lấy x = m, khi đó tồn tại y1; y2 > 0 để
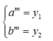
Dễ thấy y1 < y2 ⇒ am < bm ⇒ a < b
Vậy b > a > c.
Chọn A

Chọn B
Đồ thị đi lên khi ![]()
Đồ thị đi qua điểm (0;c-1) có tung độ nằm phía trên trục hoành nên c - 1 > 0 ⇔ c > 1
Đồ thị hàm số có 3 điểm cực trị nên (a-1).(b+2) < 0 mà a > 1 nên b + 2 < 0 ⇔ b < -2

Đáp án: A.
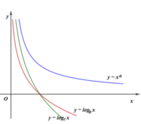
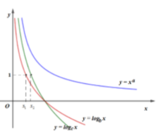
Nhận xét rằng hàm số dạng 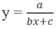 (a, b ≠ 0) có tiệm cận đứng là
(a, b ≠ 0) có tiệm cận đứng là 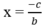 và tiệm cận ngang là y = 0.
và tiệm cận ngang là y = 0.