Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(A=\dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}\)
Ta có:
\(A>\dfrac{a}{a+b+c}+\dfrac{b}{a+b+c}+\dfrac{c}{a+b+c}\)\(=\dfrac{a+b+c}{a+b+c}=1\left(1\right)\)
\(A< \dfrac{a+b}{a+b+c}+\dfrac{b+c}{a+b+c}+\dfrac{c+a}{a+b+c}\)
\(=\dfrac{a+b+b+c+c+a}{a+b+c}=\dfrac{2\left(a+b+c\right)}{a+b+c}=2\left(2\right)\)
Từ \((1);(2)\) ta có \(1< A< 2\)
Vậy \(A\) không phải là số nguyên

Giải:
\(a,b\) là các số dương \(\Leftrightarrow\dfrac{a}{b}>0\)
Không giảm tính tổng quát
Ta giả sử \(a\ge b\Leftrightarrow a=b+m\left(m\ge0\right)\)
Ta có:
\(\dfrac{a}{b}+\dfrac{b}{a}=\dfrac{b+m}{b}+\dfrac{b}{b+m}\)
\(=1+\dfrac{m}{b}+\dfrac{b}{b+m}\ge1+\dfrac{m}{b+m}+\dfrac{b}{b+m}\)
\(=1+\dfrac{m+b}{b+m}=1+1=2\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}m=0\\a=b\end{matrix}\right.\)
Vậy \(\dfrac{a}{b}+\dfrac{b}{a}\ge2\) (Đpcm)
Nhận xét:
Trong một BĐT có chứa chữ, nếu các chữ \(a\) và \(b\) có vai trò như nhau, ta có thể thay \(a\) bởi \(b\); \(b\) bởi \(a\), do đó ta có thể sắp thú tự tùy ý cho nên trong cách giải trên ta đã giả sử \(a\ge b\) mà không sợ mất tính tổng quát.

Câu 2:
\(\Leftrightarrow x\left(\dfrac{1}{6}+\dfrac{1}{10}+\dfrac{1}{15}+...+\dfrac{1}{78}\right)=\dfrac{220}{39}\)
\(\Leftrightarrow2x\left(\dfrac{1}{12}+\dfrac{1}{20}+...+\dfrac{1}{156}\right)=\dfrac{220}{39}\)
\(\Leftrightarrow x\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+...+\dfrac{1}{12}-\dfrac{1}{13}\right)=\dfrac{110}{39}\)
\(\Leftrightarrow x\cdot\dfrac{10}{39}=\dfrac{110}{39}\)
=>x=11

+\(\frac{a}{b+c}>\frac{a}{a+b+c}\)
\(\frac{b}{a+c}>\frac{b}{a+b+c}\)
\(\frac{c}{a+b}>\frac{c}{a+b+c}\) cộng lại ta được
=>\(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}>1\)
+\(\frac{a}{b+c}< \frac{a+a}{a+b+c}\)
\(\frac{b}{a+c}< \frac{b+b}{a+b+c}\)
\(\frac{c}{a+b}< \frac{c+c}{a+b+c}\) cộng lại
=> \(\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}< 2\)
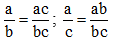
Lời giải:
Ta có:
\(\frac{a}{b+c}=\frac{2a}{2(b+c)}=\frac{2a}{(b+c)+(b+c)}< \frac{2a}{a+b+c}\) (do mỗi số nhỏ hơn tổng hai số kia thì \(a< b+c\))
Hoàn toàn tương tự:
\(\left\{\begin{matrix} \frac{b}{c+a}< \frac{2b}{a+b+c}\\ \frac{c}{a+b}< \frac{2c}{a+b+c}\end{matrix}\right.\)
Cộng theo vế các BĐT vừa thu được ta có:
\(\frac{a}{b+c}+\frac{b}{c+a}+\frac{c}{a+b}< \frac{2a}{a+b+c}+\frac{2b}{a+b+c}+\frac{2c}{a+b+c}=2\)
Ta có đpcm.