Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt vế trái BĐT cần chứng minh là P
Áp dụng BĐT \(\dfrac{1}{x}+\dfrac{1}{y}\ge\dfrac{4}{x+y}\) ( Tự chứng minh BĐT này ), ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}\ge\dfrac{4}{a+b}\)
\(\Rightarrow\dfrac{1}{\dfrac{1}{a}+\dfrac{1}{b}}\le\dfrac{1}{\dfrac{4}{a+b}}=\dfrac{a+b}{4}\left(1\right)\)
Tương tự: \(\dfrac{1}{\dfrac{1}{b}+\dfrac{1}{c}}\le\dfrac{b+c}{4}\left(2\right)\)
\(\dfrac{1}{\dfrac{1}{c}+\dfrac{1}{a}}\le\dfrac{c+a}{4}\left(3\right)\)
Cộng \(\left(1\right),\left(2\right),\left(3\right)\) vế theo vế, ta được:
\(P\le\dfrac{a+b+b+c+c+a}{4}=\dfrac{a+b+c}{2}\)
Dấu ''='' xảy ra khi và chỉ khi a=b=c

Có gì đâu nhỉ?
Cauchy-Schwarz:
\(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{\left(1+1+1\right)^2}{2\left(a+b+c\right)}=\dfrac{9}{2\left(a+b+c\right)}=\dfrac{4,5}{a+b+c}>\dfrac{3}{a+b+c}\)
áp dụng BĐT cauchy- schwarz ta có
\(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{\left(1+1+1\right)^2}{2\left(a+b+c\right)}\)
⇔ \(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{9}{2\left(a+b+c\right)}\)
⇔ \(\dfrac{1}{a+b}+\dfrac{1}{b+c}+\dfrac{1}{c+a}\ge\dfrac{3}{a+b+c}\) (đpcm)

Đặt \(P=\dfrac{1}{a^3\left(b+c\right)}+\dfrac{1}{b^3\left(c+a\right)}+\dfrac{1}{c^3\left(a+b\right)}\)
\(P=\dfrac{\left(abc\right)^2}{a^3\left(b+c\right)}+\dfrac{\left(abc\right)^2}{b^3\left(c+a\right)}+\dfrac{\left(abc\right)^2}{c^3\left(a+b\right)}\)
\(P=\dfrac{\left(bc\right)^2}{a\left(b+c\right)}+\dfrac{\left(ca\right)^2}{b\left(c+a\right)}+\dfrac{\left(ab\right)^2}{c\left(a+b\right)}\)
\(P\ge\dfrac{\left(bc+ca+ab\right)^2}{a\left(b+c\right)+b\left(c+a\right)+c\left(a+b\right)}\) (BĐT B.C.S)
\(=\dfrac{ab+bc+ca}{2}\) \(\ge\dfrac{3\sqrt[3]{abbcca}}{2}=\dfrac{3}{2}\) (do \(abc=1\)).
ĐTXR \(\Leftrightarrow a=b=c=1\)

thử bài bất :D
Ta có: \(\dfrac{1}{a^3\left(b+c\right)}+\dfrac{a}{2}+\dfrac{a}{2}+\dfrac{a}{2}+\dfrac{b+c}{4}\ge5\sqrt[5]{\dfrac{1}{a^3\left(b+c\right)}.\dfrac{a^3}{2^3}.\dfrac{\left(b+c\right)}{4}}=\dfrac{5}{2}\) ( AM-GM cho 5 số ) (*)
Hoàn toàn tương tự:
\(\dfrac{1}{b^3\left(c+a\right)}+\dfrac{b}{2}+\dfrac{b}{2}+\dfrac{b}{2}+\dfrac{c+a}{4}\ge5\sqrt[5]{\dfrac{1}{b^3\left(c+a\right)}.\dfrac{b^3}{2^3}.\dfrac{\left(c+a\right)}{4}}=\dfrac{5}{2}\) (AM-GM cho 5 số) (**)
\(\dfrac{1}{c^3\left(a+b\right)}+\dfrac{c}{2}+\dfrac{c}{2}+\dfrac{c}{2}+\dfrac{a+b}{4}\ge5\sqrt[5]{\dfrac{1}{c^3\left(a+b\right)}.\dfrac{c^3}{2^3}.\dfrac{\left(a+b\right)}{4}}=\dfrac{5}{2}\) (AM-GM cho 5 số) (***)
Cộng (*),(**),(***) vế theo vế ta được:
\(P+\dfrac{3}{2}\left(a+b+c\right)+\dfrac{2\left(a+b+c\right)}{4}\ge\dfrac{15}{2}\) \(\Leftrightarrow P+2\left(a+b+c\right)\ge\dfrac{15}{2}\)
Mà: \(a+b+c\ge3\sqrt[3]{abc}=3\) ( AM-GM 3 số )
Từ đây: \(\Rightarrow P\ge\dfrac{15}{2}-2\left(a+b+c\right)=\dfrac{3}{2}\)
Dấu "=" xảy ra khi a=b=c=1
1. \(a^3+b^3+c^3+d^3=2\left(c^3-d^3\right)+c^3+d^3=3c^3-d^3\) :D

Xét hiệu VT - VP
\(\dfrac{a+b}{bc+a^2}+\dfrac{b+c}{ab+b^2}+\dfrac{c+a}{ab+c^2}-\dfrac{1}{a}-\dfrac{1}{b}-\dfrac{1}{c}=\dfrac{a^2+ab-bc-a^2}{a\left(bc+a^2\right)}+\dfrac{b^2+bc-ac-b^2}{b\left(ac+b^2\right)}+\dfrac{c^2+ac-ab-c^2}{c\left(ab+c^2\right)}=\dfrac{b\left(a-c\right)}{a\left(bc+a^2\right)}+\dfrac{c\left(b-a\right)}{b\left(ac+b^2\right)}+\dfrac{a\left(c-b\right)}{c\left(ab+c^2\right)}\)
Do a,b,c bình đẳng nên giả sử a\(\ge\)b\(\ge\)c, khi đó \(b\left(a-c\right)\)\(\ge\)0, c(b-a)\(\le\)0, a(c-b)\(\le\)0
\(a^3\ge b^3\ge c^3=>abc+a^3\ge abc+b^3\ge abc+c^3\)=>\(\dfrac{b\left(a-c\right)}{a\left(bc+a^2\right)}\le\dfrac{b\left(a-c\right)}{b\left(ac+b^2\right)}\)
=> VT -VP \(\le\) \(\dfrac{b\left(a-c\right)}{a\left(bc+a^2\right)}+\dfrac{c\left(b-a\right)}{b\left(ac+b^2\right)}+\dfrac{a\left(c-b\right)}{c\left(ab+c^2\right)}=\dfrac{ab-ac}{b\left(ac+b^2\right)}+\dfrac{ac-ab}{c\left(ab+c^2\right)}=\dfrac{a\left(b-c\right)}{b\left(ac+b^2\right)}-\dfrac{a\left(b-c\right)}{c\left(ab+c^2\right)}\)
mà \(\dfrac{1}{b\left(ac+b^2\right)}\le\dfrac{1}{c\left(ab+c^2\right)}\) nên VT-VP <0 đpcm

áp dụng BĐT:
1/a +1/b+1/c>= 9/a+b+c mà a+b+c=1
=>1/a+1/b+1/c≥9

Ta có:
\(\dfrac{1}{a+3b}+\dfrac{1}{c+3}\ge\dfrac{4}{a+3b+c+3}=\dfrac{4}{2b+6}=\dfrac{2}{b+3}\)
Tương tự:
\(\dfrac{1}{b+3c}+\dfrac{1}{a+3}\ge\dfrac{2}{c+3}\)
\(\dfrac{1}{c+3a}+\dfrac{1}{b+3}\ge\dfrac{2}{a+3}\)
Cộng vế:
\(\sum\dfrac{1}{a+3b}+\sum\dfrac{1}{a+3}\ge\sum\dfrac{2}{a+3}\)
\(\Rightarrow\sum\dfrac{1}{a+3b}\ge\sum\dfrac{1}{a+3}\) (đpcm)
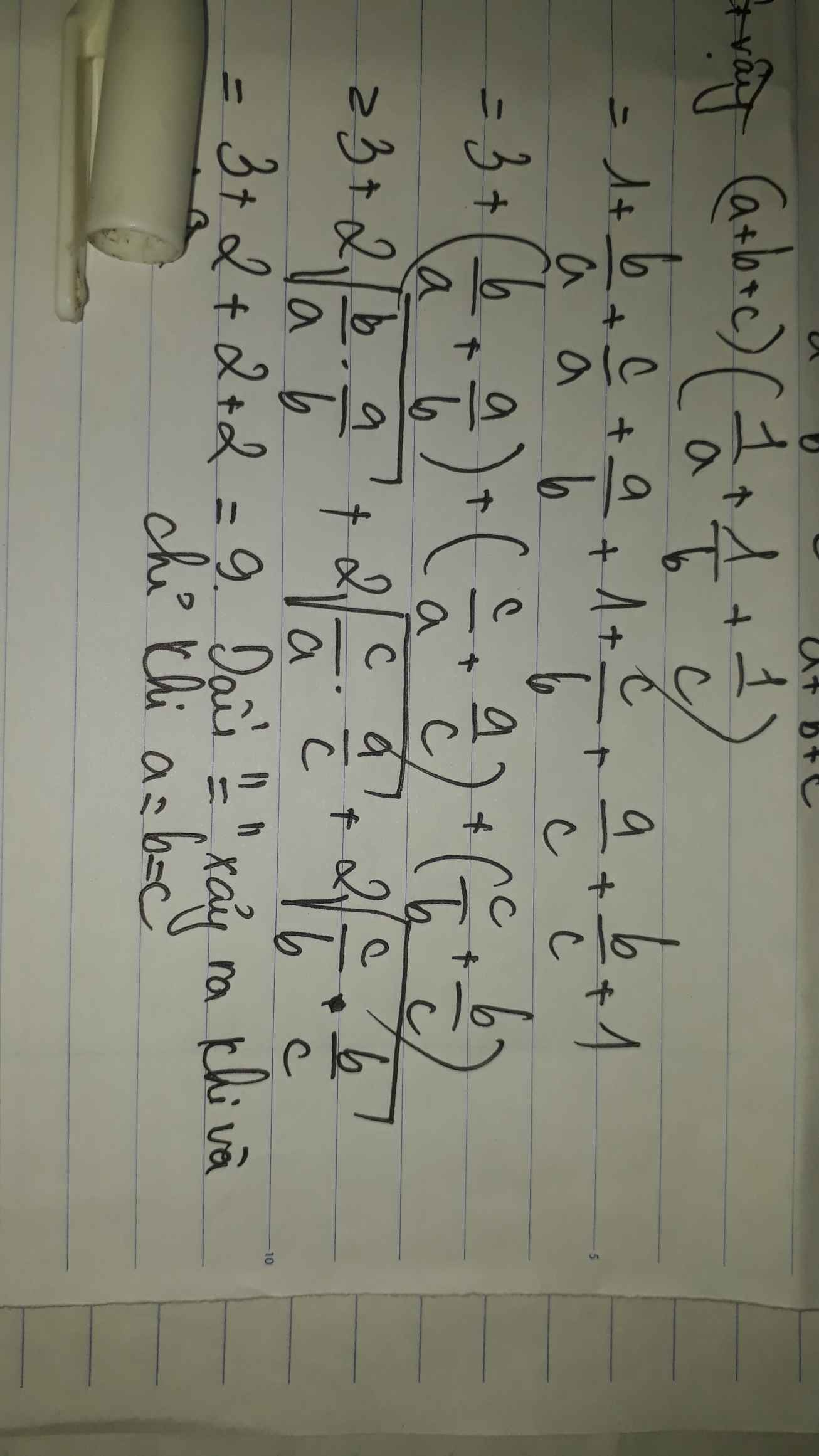

Ta có :
\(a+b+c=1\)
\(\Leftrightarrow\) \(\dfrac{a+b+c}{a}=\dfrac{1}{a}\)
\(\Leftrightarrow1+\dfrac{b}{a}+\dfrac{c}{a}=\dfrac{1}{a}\)(1)
Tương tự ta lại có :
\(1+\dfrac{a}{b}+\dfrac{c}{b}=\dfrac{1}{b}\) (2)
\(1+\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{1}{c}\) (3)
Từ 1 ; 2 và 3 :
\(\left\{{}\begin{matrix}1+\dfrac{b}{a}+\dfrac{c}{a}=\dfrac{1}{a}\\1+\dfrac{a}{b}+\dfrac{c}{b}=\dfrac{1}{b}\\1+\dfrac{a}{c}+\dfrac{b}{c}=\dfrac{1}{c}\end{matrix}\right.\)
Cộng vế theo vế ta được :
\(3+\left(\dfrac{a}{b}+\dfrac{b}{a}\right)+\left(\dfrac{b}{c}+\dfrac{c}{b}\right)+\left(\dfrac{c}{a}+\dfrac{a}{c}\right)=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
căng thế @Dương Phan Khánh Dương
Cauchy-Schwarz: \(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{\left(1+1+1\right)^2}{a+b+c}=9\)