
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Ta có:
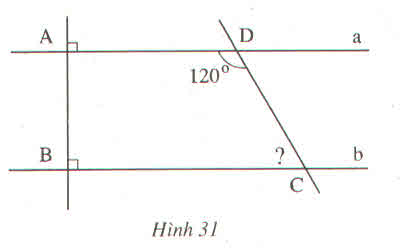
AB \(\perp\) a
AB \(\perp\) b
\(\Rightarrow\)a // b
b, Ta có: a // b( câu a)
hai góc ADC và DCB là hai góc trong cùng phía
\(\Rightarrow\)DCB = 180\(^0\) - ADC(tính chất hai đường thẳng song song)
\(\Rightarrow\) DCB = 180\(^0\)-120\(^0\) = 60\(^0\)

đây là cậu chép trg chỗ giải đáp rồi mà mk ko đc lm giống trg giải đáp



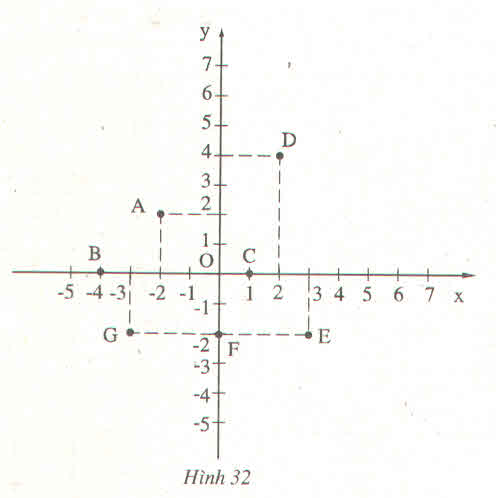
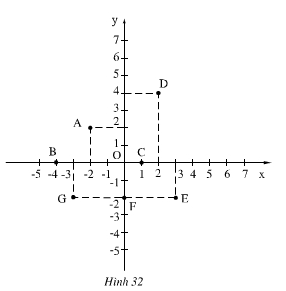
Ta có tọa độ các điểm: A(-2; 2); B(-4; 0); C(1; 0); D(2; 4); E(3; -2); F(0; -2); G(-3; -2)

a. 2a = 3b = 4c và a - b + c = 10
ta có
\(\dfrac{a}{3}=\dfrac{b}{2}\Rightarrow\dfrac{a}{6}=\dfrac{b}{4}\)
\(\dfrac{b}{4}=\dfrac{c}{3}\)
=>\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}\) và a-b+c=10
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}\) =>\(\dfrac{a-b+c}{6-4+3}=\dfrac{10}{5}=2\)
=>\(\dfrac{a}{6}=2\Rightarrow a=12\)
\(\dfrac{b}{4}=2\Rightarrow b=8\)
\(\dfrac{c}{3}=2\Rightarrow c=6\)
vậy a=12;b=8;c=6
1.
a, Ta có : \(\dfrac{a}{12}=\dfrac{b}{8}=\dfrac{c}{6}\)( bt cách lm chứ )
Dựa vào tính chất của dãy tỉ số = nhau ( bn tự tính nhé !!! )
b,Ta có : \(\dfrac{a}{30}=\dfrac{b}{18}=\dfrac{c}{15}\) ( nt )
Cx dựa vào tính chất của dãy tỉ số = nhau
2.
a, Ta có : a/3 = b/4 = ( 2c ) / 8
Cx làm nt nhé !!!
b, Ta có : b/6 = a/21 = c/10
cx lm nt nhé !!!
Sr mk đang bận mk k giải gợi ý cho bạn nha

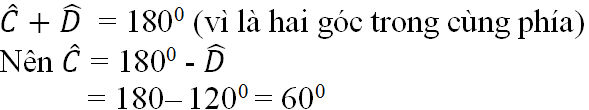











Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{a}{2b}=\dfrac{b}{2c}=\dfrac{c}{2a}=\dfrac{a+b+c}{2(a+b+c)}=\dfrac{1}{2} \\->a=\dfrac{1}{2}.2b=b \\b=\dfrac{1}{2}.2c=c \\c=\dfrac{1}{2}.2a=a \\->a=b=c (đpcm)\)