Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ O1 kẻ O1H vuông góc với O2C tại H. Vì R2 > R1 nên ta được O1BCH là hình chữ nhật
và : O2H = R2 - R1 = 2
\(cos\widehat{O_1O_2H}=\frac{O_2H}{O_1O_2}=\frac{2}{8}=\frac{1}{4}\Rightarrow\widehat{O_1O_2H}=\alpha\)(Bạn bấm máy tính để tìm giá trị góc này, còn mình đặt là \(\alpha\)cho dễ nhìn)
\(\Rightarrow\widehat{BO_1O_2}=180^o-\alpha\)(BO1 // CO2)
\(AB=\sqrt{2R^2_1-2R_1^2.cos\left(180^o-\alpha\right)}=m\)
\(AC=\sqrt{2R_2^2-2R_2^2.cos\alpha}=n\)
Gọi \(S_1\) và \(S_2\) lần lượt là diện tích hình quạt \(O_1AB\) và \(O_2AC\) thì ta có :
\(S_1=\frac{\pi.R_1^2.\left(180^o-\alpha\right)}{360^o}\) ; \(S_2=\frac{\pi.R_2^2.\alpha}{360^o}\)
\(S_{\Delta O_1AB}=\frac{1}{2}.R_1^2.sin\left(90^o-\alpha\right)\); \(S_{\Delta O_2AC}=\frac{1}{2}R_2^2.sin\alpha\)
Diện tích hình viên phân giới hạn bởi AB là : \(S'=S_1-S_{\Delta O_1AB}=x\)
Diện tích hình viên phân giới hạn bởi AC là : \(S''=S_2-S_{\Delta O_2AC}=y\)
Diện tích tam giác ABC nằm ngoài cả hai đường tròn đã cho là :
\(S_{ABC}-S'-S''=\frac{1}{2}m.n-x-y\)

bài này dễ mà
có nhiêu cách tính lắm
mik sẽ trình bày một cách nha !!!
gọi O là tâm của đường tròn ngoại tiếp tam giác ABC
ta có : tam giác ABC cân taỊ A
mà AO= 1/2 BC=\(3\sqrt{2}\)
nên AO là đường trung tuyến của tam giác ABC
ĐỒNG THỜI CŨNG LÀ ĐƯỜNG cao của tam giác ABC
ta lại có : BC=2R=2*\(3\sqrt{2}\)=6\(\sqrt{2}\)
S của tam giác ABC= 1/2 *AO*BC=1/2*\(3\sqrt{2}\cdot6\sqrt{2}\)=18
vậy diện tich tam giác là 18

BÀI LÀM
a, xét tứ giác ADOE có:
góc A= góc E=góc D=90O
mà ta thấy: OE=OD( bán kính = nhau)
vậy tứ giác ADOE là hình vuông (dhnb)
a) Dễ thấy tứ giác AEOD là hình chữ nhật (tứ giác có 3 góc vuông).
Mà OD = OE ( cùng bằng bán kính đường tròn nội tiếp tam giác ABC).
Nên tứ giác AEOD là hình vuông.
b) Gọi H là chân đường vuông góc kẻ từ O xuống BC.
Có SΔABC=SΔOAB+SΔOBC+SΔOAC
=12 OD.AB+12 OE.AC+12 OH.BC
=12 r.(AB+AC+BC)
=12 pr (pp là chu vi của tam giác ABCABC, rr là bán kính đường tròn nội tiếp).
c) Áp dụng định lý Pi-ta-go ta có: BC=√AB2+AC2=10(cm).
Diện tích tam giác ABC là: 12 AB.AC=12 .6.8=24(cm2).
Chu vi tam giác ABC là: 6+8+10=24(cm).
Suy ra: 24=12 .24.r⇔r=2(cm).
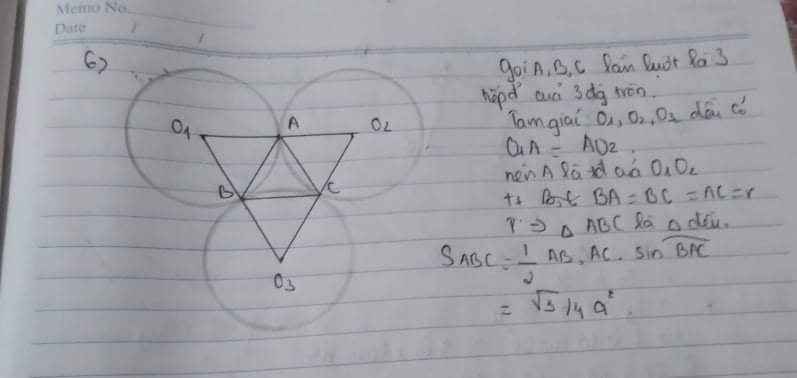
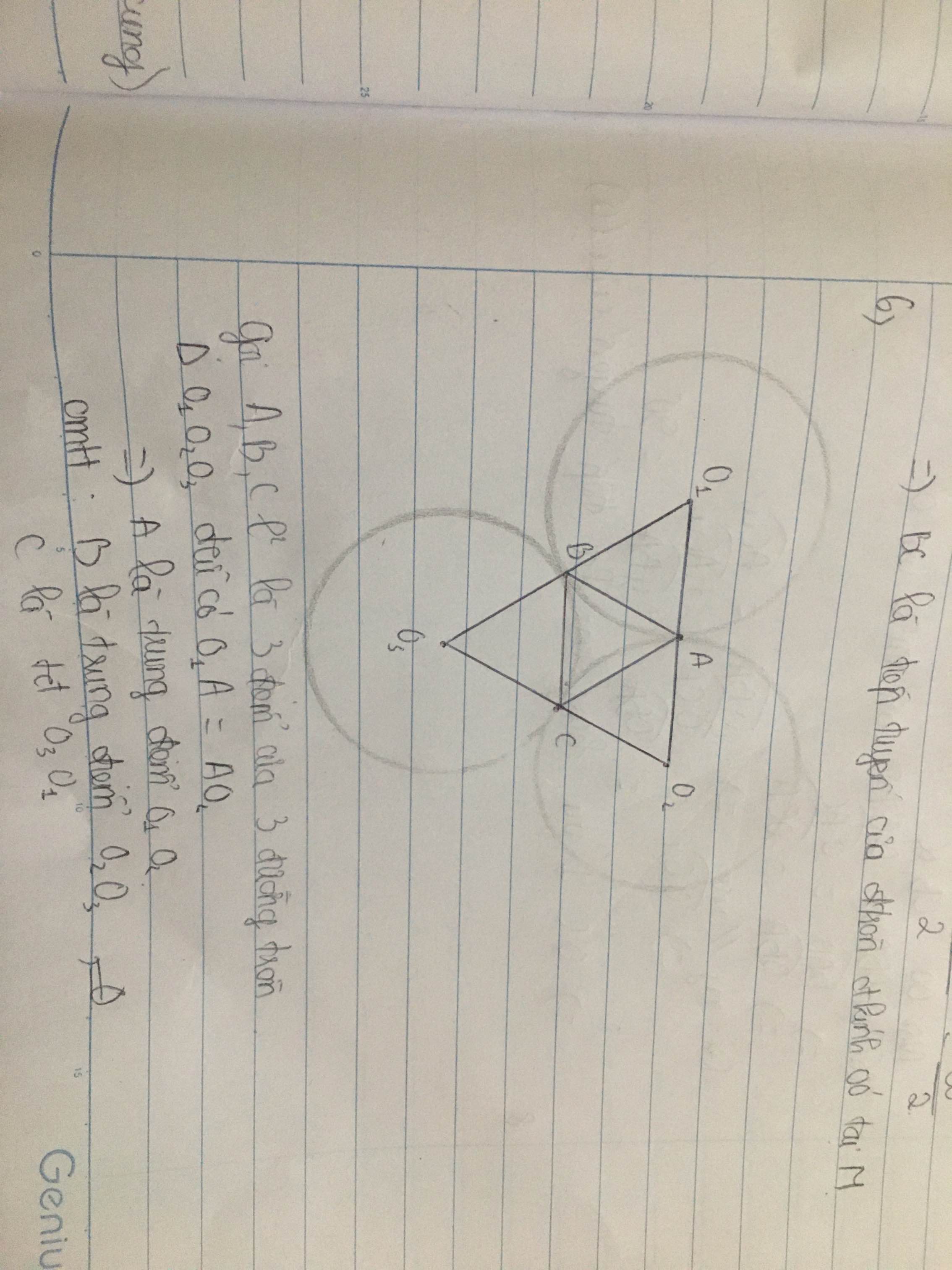
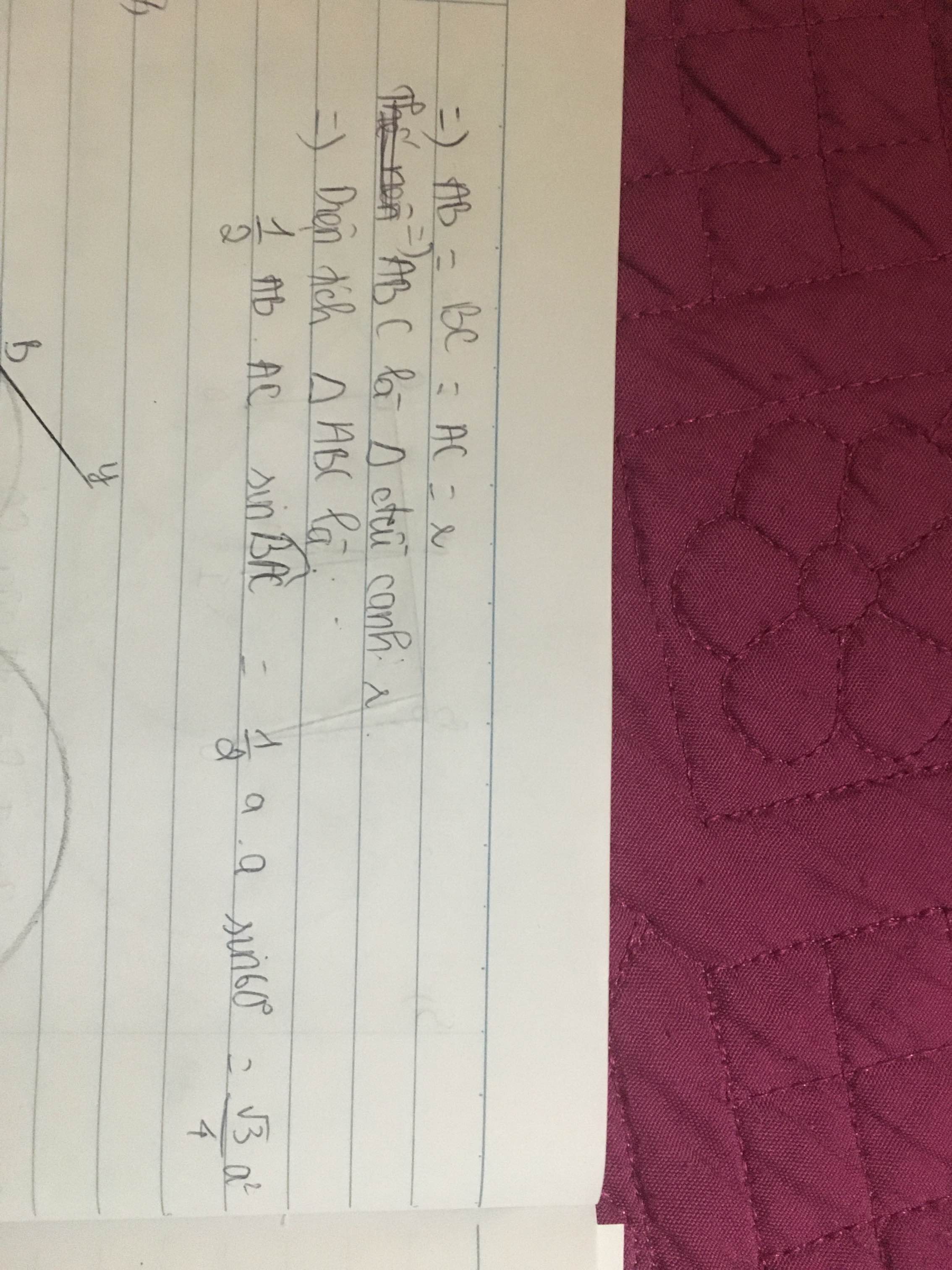
A B C M N P
GỌI TÂM CÁC HÌNH TRÒN LẦN LƯỢT LÀ M , N , P
KHI ĐÓ TA CÓ TAM GIÁC MNP LÀ TAM GIÁC ĐỀU VÀ A , B , C LÀ TRUNG ĐIỂM CỦA MỖI CẠNH CỦA TAM GIÁC VÀ MỖI CẠNH CÓ ĐỘ DÀI BẰNG ĐƯỜNG HÌNH TRÒN
TA CÓ S ANC = S AMB = S BCP = 1/4 S ( N ) = \(\frac{1}{4}.18\pi=\frac{9}{2}\pi\)
TA CÓ TAM GIÁC MNP LÀ TAM GIÁC ĐỀU CÓ CẠNH = \(6\sqrt[]{2}\)
=> S MNP = \(\frac{\sqrt{3}}{4}.72=18\sqrt{3}\)
=> S ABC = \(18\sqrt{3}-\frac{27}{2}\pi\)