Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

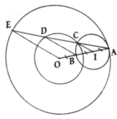
a, Gọi I là trung điểm của AB, ta có: OI = OA – IA
b, Ta chứng minh được IC//BD//OE
Mà OB = BI = IA => AC = CD = DE

a) Tam giác ABC nội tiếp đường tròn (O) đường kính BC
=> OA=OB=OC và O là trung điểm của BC
=> Tam giác ABC vuông tại A
=> góc BAC = 90 độ
b) DO tam giác HAK nội tiếp đường tròn (I)
Lại có góc HAK = 90 độ
=> HK là đường kính của (I)
=> HK đi qua I
=> H,I,K thẳng hàng
c) Đề bài ghi ko rõ
d) 3 điểm nào?

b: Xét ΔBHA có
BD vừa là đường cao, vừa là phân giác
=>ΔBHA cân tại B
=>D là trung điểm của AH
góc EAD=1/2*sđ cung AD
góc FAD=góc FBC=1/2*sđ cung DC
mà sđ cung AD=sđ cung DC
nên góc EAD=góc FAD
=>AD là phân giác của góc EAF
=>D là trung điểm của EF
Xét tứ giác AEHF có
D là trung điểm chung của AH và EF
AH vuông góc EF
=>AEHF là hình thoi
a: góc ADB=1/2*180=90 độ
=>BD vuông góc AH
góc ACB=1/2*180=90 độ
=>AC vuông góc HB
góc HDF+góc HCF=180 độ
=>HDFC nội tiếp