Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a+b=1\Leftrightarrow b=1-a\\ \Leftrightarrow P=a^2+1-a=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ P_{min}=\dfrac{3}{4}\Leftrightarrow a=\dfrac{1}{2}\Leftrightarrow b=\dfrac{1}{2}\)

y'=1/3*3x^2+1/2*2x(m-1)+(2m-1)
=x^2+x(m-1)+2m-1
a: y đồng biến trên R thì y'>0 với mọi x thuộc R
Δ=(m-1)^2-4(2m-1)
=m^2-2m+1-8m+4=m^2-10m+5
Để y'>0 với mọi x thuộc R thì m^2-10m+5<0
=>5-2*căn 5<m<5+2căn 5
b: y đồng biến trên (-vô cực;-2) và (0;1) khi y'>0 với mọi x thuộc (-vô cực;-2) và (0;1)
y'=x^2+x(m-1)+2m-1
=x^2+xm-x+2m-1
=m(x+2)+x^2-x-1
y'>0 với x thuộc (-vô cực;-2)
=>m>-x^2+x+1/(x+2) với x thuộc (vô cực;-2)
g(x)=-x^2+x+1/(x+2)
g'=(-x^2+x+1)'(x+2)-(-x^2+x+1)(x+2)'/(x+2)^2
=(x+2+x^2-x-1)/(x+2)^2=(x^2+1)/(x+2)^2>0 với mọi x
=>m thuộc (-vô cực;-2)
Tương tự, ta cũng được: m thuộc (0;1)

Chọn A
Hàm số f(x) = (x-6) x 2 + 4 xác định và liên tục trên đoạn [0;3].
![]()
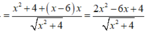

![]()
Suy ra ![]()
![]()
![]() với a là số nguyên và b, c là các số nguyên dương nên
với a là số nguyên và b, c là các số nguyên dương nên
a = - 12, b = 3, c = 13. Do đó: S = a + b + c = 4.