Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

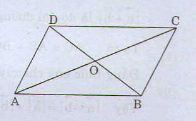
a/ \(\left|\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}+\overrightarrow{OD}\right|=\left|\overrightarrow{0}+\overrightarrow{0}\right|=0\)
b/ \(\left|\overrightarrow{OA}+\overrightarrow{OB}\right|+\left|\overrightarrow{OC}+\overrightarrow{OD}\right|=a+a=2a\)
c/
\(\left|\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OB}\right|+\left|\overrightarrow{OD}\right|=\left|\overrightarrow{OB}\right|+\left|\overrightarrow{OD}\right|=2\left|\overrightarrow{OB}\right|=2\sqrt{a^2-\frac{a^2}{4}}=a\sqrt{3}\)

\(\overrightarrow{AC}-\overrightarrow{AD}=\overrightarrow{AC}-\overrightarrow{BC}=\overrightarrow{AC}+\overrightarrow{CB}=\overrightarrow{AB}\)
Đáp án A đúng

A B C D O M N E F
a) Giả sử \(\overrightarrow{OA}+\overrightarrow{OC}=\overrightarrow{OB}+\overrightarrow{OD}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{OC}-\overrightarrow{OB}-\overrightarrow{OD}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{OA}+\overrightarrow{BO}+\overrightarrow{OC}+\overrightarrow{DO}=\overrightarrow{0}\)
\(\Leftrightarrow\left(\overrightarrow{BO}+\overrightarrow{OA}\right)+\left(\overrightarrow{DO}+\overrightarrow{OC}\right)=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\) (đúng do tứ giác ABCD là hình bình hành).
b) \(\overrightarrow{ME}+\overrightarrow{FN}=\overrightarrow{MA}+\overrightarrow{AE}+\overrightarrow{FC}+\overrightarrow{CN}\)
\(=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\).
Do các tứ giác AMOE, MOFB, OFCN, EOND cũng là các hình bình hành.
Vì vậy \(\overrightarrow{CN}=\overrightarrow{FO}=\overrightarrow{BM};\overrightarrow{FC}=\overrightarrow{ON}=\overrightarrow{ED}\).
Do đó: \(\overrightarrow{ME}+\overrightarrow{FN}=\left(\overrightarrow{MA}+\overrightarrow{CN}\right)+\left(\overrightarrow{AE}+\overrightarrow{FC}\right)\)
\(=\left(\overrightarrow{MA}+\overrightarrow{BM}\right)+\left(\overrightarrow{AE}+\overrightarrow{ED}\right)\)
\(=\overrightarrow{BA}+\overrightarrow{AD}=\overrightarrow{BD}\) (Đpcm).
Câu a là 4 vecto cộng lại bằng vecto 0 nha mấy bạn :((