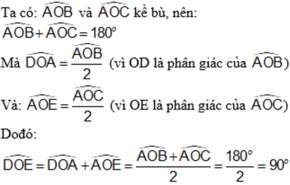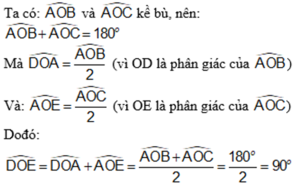Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Ta có : ∠AOB + ∠BOC = 180o ( Hai góc kề bù ) .
⇒ 80o + ∠BOC = 180o .
⇒ ∠BOC = 180o - 80o .
⇒ ∠BOC = 100o .
Vì tia OD là tia phân giác của ∠AOB nên tia OD nằm giữa hai tia OB và OA và :
∠AOD = ∠DOB = ∠AOB 2∠AOB 2.
= 80o2=40o.80o2=40o.
Vì tia OD nằm giữa hai tia OA và OB mà tia OE nằm trong ∠BOC nên tia OB nằm giữa hai tia OD và OE .
⇒ ∠DOB + ∠BOE = ∠DOE .
⇒ 40o + ∠BOE = 90o ( vì tia OE vuông góc với tia OD nên ∠DOE = 90o ) .
⇒ ∠BOE = 90o - 40o .
⇒ ∠BOE = 50o .
b, Vì tia OE nằm trong ∠BOC nên tia OE nằm giữa hai tia OB avf OC nên :
Ta có : ∠BOE + ∠COE = ∠BOC .
⇒ 50o + ∠COE = 100o .
⇒ ∠COE = 100o - 50o .
⇒ ∠COE = 50o .
Vì ∠BOE = ∠COE và tia OE nằm giữa hai tia OB và OC nên tia OE là tia phân giác của ∠BOC .
Vậy bài toán được chứng minh .

Ủa phải có số đo của mấy góc này cụ thể chứ không có sao mà làm
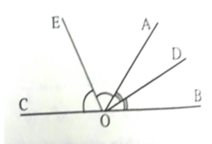
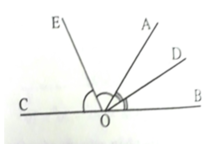
Vì ^AOB và ^AOC kề bù => ^AOB + ^AOC = 1800 ( 1 )
Có ^DOE = ^AOD + ^AOE do D và E nằm khác nửa mặt phẳng bờ OA ( 2 )
^AOD = ^AOB : 2 do AD là tia phân giác ^AOB ( 3 )
^AOE = ^AOC : 2 do AE là tia phân giác ^AOE ( 4 ). Từ ( 1 )( 2 )( 3 )( 4 )
=> ^DOE = ^AOD + ^AOE = ^AOB : 2 + ^AOC : 2 = ( ^AOB + ^AOC ) : 2
= 1800 : 2 = 900. Vậy ^DOE = 900