K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

26 tháng 7 2017
H la giao diem cua AB va CD ta co AH = BH =1/2 AB =12cm
cH=DH=6cm
=> AC=AD =\(\sqrt{12^2+6^2}\)=\(6\sqrt{5}\)......................

GN
3 tháng 6 2018
ta có: ON = 8 = OM + MN => OM = ON - MN
và: O'M = 6 = O'N + MN => O'N = O'M - MN
mà: O'O = OM + MN + NO' = 11
=> O'O= ON - MN + MN + O'M - MN
= ON + O'M - MN
Thay vào, ta được: 11= 8+ 6 - MN => MN =3
Vậy MN = 3 cm
11 =

CM
22 tháng 6 2019
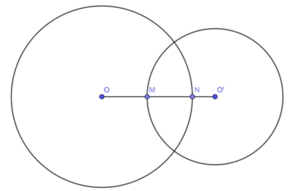
Ta có:
ON = 8cm, O'M = 6cm, OO' = 10cm
ON + O'M = OM + MN + MN + O'N = (OM + MN + O'N) + MN = OO' + MN
⇒ 8 + 6 = 10 + MN ⇒ MN = 4cm
Đáp án: D