Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
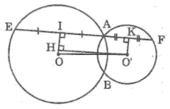
Kẻ OI ⊥ AE, O’K ⊥ AF
Trong đường tròn (O), ta có:
IA = IE = (1/2).AE (đường kính vuông góc với dây cung)
Trong đường tròn (O’), ta có:
KA = KF = (1/2).AF (đường kính vuông góc với dây cung)
Ta có: EF = AE = AF
Suy ra: EF = 2IA = 2AK = 2(IA + AK) = 2IK (1)
Kẻ O’H ⊥ OI
Khi đó tứ giác IHO’K là hình chữ nhật (có ba góc vuông)
Suy ra: O’H = IK
Trong tam giác OHO’ ta có: O’H ≤ OO’ = 3 (cm)
Suy ra: IK ≤ OO’ (2)
Từ (1) và (2) suy ra: EF ≤ 2OO’ = 6 (cm)
Ta có EF = 6cm khi H và O trùng nhau hay EF // OO’
Vậy EF có độ dài lớn nhất bằng 6cm khi và chỉ khi EF // OO’
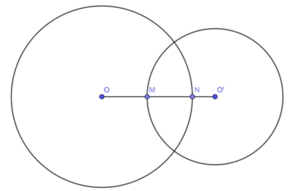
Ta có:
ON = 8cm, O'M = 6cm, OO' = 10cm
ON + O'M = OM + MN + MN + O'N = (OM + MN + O'N) + MN = OO' + MN
⇒ 8 + 6 = 10 + MN ⇒ MN = 4cm
Đáp án: D
a: góc BMA=góc CNA=90 độ
=>MB//NC
=>IK//MB//NC
=>IK vuông góc MN
góc AIK+góc AHK=90+90=180 độ
=>AHIK nội tiếp
b: ΔHMN đồng dạng với ΔABC
=>góc MHN=góc BAC cố định
\(S_{HMN}=\dfrac{1}{2}\cdot HM\cdot HN\cdot sin\widehat{MHN}< =\dfrac{1}{2}\cdot AB\cdot AC\cdot sin\widehat{BAC}\)
Dấu = xảy ra khi MH là đừog kính của (O) và NH là đường kính của (O')
ta có: ON = 8 = OM + MN => OM = ON - MN
và: O'M = 6 = O'N + MN => O'N = O'M - MN
mà: O'O = OM + MN + NO' = 11
=> O'O= ON - MN + MN + O'M - MN
= ON + O'M - MN
Thay vào, ta được: 11= 8+ 6 - MN => MN =3
Vậy MN = 3 cm
11 =
Do hai đường tròn bằng nhau nên hai cung nhỏ AB bằng nhau. Vì cùng căng dây AB.
Suy ra 
= 
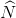(cùng chắn hai cung bằng nhau) nên tam giác BMN là tam giác cân đỉnh B