Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do A thuộc d1 nên tọa độ có dạng \(A\left(a;3a-3\right)\)
Do B thuộc d2 nên tọa độ có dạng: \(B\left(b;-b-2\right)\)
Áp dụng công thức trung điểm:
\(\Rightarrow\left\{{}\begin{matrix}a+0=2b\\3a-3+2=2\left(-b-2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a-2b=0\\3a+2b=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{3}{4}\\b=-\dfrac{3}{8}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}A\left(-\dfrac{3}{4};-\dfrac{21}{4}\right)\\B\left(-\dfrac{3}{8},-\dfrac{13}{8}\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AB}=\left(\dfrac{3}{8};\dfrac{29}{8}\right)\)
Phương trình d có dạng:
\(29x-3\left(y-2\right)=0\Leftrightarrow29x-3y+6=0\)

Lời giải:
Vì $A\in (d_1)$ nên gọi tọa độ của $A$ là $(a, 2a-2)$
Vì $B\in (d_2)$ nên gọi tọa độ của $B$ là $(b, -b-3)$
$M$ là trung điểm của $AB$ nên:
\(3=x_M=\frac{x_A+x_B}{2}=\frac{a+b}{2}\Rightarrow a+b=6(1)\)
\(0=y_M=\frac{y_A+y_B}{2}=\frac{2a-2-b-3}{2}\Rightarrow 2a-b=5(2)\)
Từ $(1); (2)\Rightarrow a=\frac{11}{3}; b=\frac{7}{3}$
Khi đó: $A=(\frac{11}{3}, \frac{16}{3})$
Vì $A, M\in (d)$ nên VTCP của (d) là $\overrightarrow{MA}=(\frac{2}{3}, \frac{16}{3})$
$\Rightarrow \overrightarrow{n_d}=(\frac{-16}{3}, \frac{2}{3})$
PTĐT $(d)$ là:
$\frac{-16}{3}(x-3)+\frac{2}{3}(y-0)=0$
$\Leftrightarrow -8x+y+24=0$

\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;0\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(m;-1\right)\) là 1 vtpt
Để góc giữa 2 đường thẳng bằng 45 độ
\(\Rightarrow cos\left(d_1;d_2\right)=cos45^0=\dfrac{\left|1.m-0.1\right|}{\sqrt{1^2+0^2}.\sqrt{m^2+\left(-1\right)^2}}\)
\(\Leftrightarrow\dfrac{1}{\sqrt{2}}=\dfrac{\left|m\right|}{\sqrt{m^2+1}}\Leftrightarrow m^2+1=2m^2\)
\(\Rightarrow m=\pm1\)
Có 2 giá trị m

(d1) : y= -x-1 ; (d2) : y=x/2 +1
Gọi (d) : y =ax +b đi qua M(1;0)
=> 0 = a+b => b=-a => (d) : y=ax-a
Xét phương trình hoành độ giao điểm của (d1) và (d) ta có:
-x-1 = ax-a
<=> x(a+1) = a-1
<=> x= (a-1)/(a+1) ( a khác -1)
=> \(A\left(\dfrac{a-1}{a+1};\dfrac{-2a}{a+1}\right)\)
\(\Rightarrow MA^2=\left(\dfrac{a-1}{a+1}-1\right)^2+\left(\dfrac{-2a}{a+1}\right)^2=\dfrac{4a^2+4}{a^2+2a+1}\left(1\right)\)
Xét phương trình hoành độ giao điểm chung giữa (d) và (d2) ta có:
x/2 + 1 =ax-a
<=> x+2 = 2ax-2a
<=> x(2a-1) = 2a+2
<=> x= (2a+2) / (2a-1) ( a khác 1/2)
=> \(B\left(\dfrac{2a+2}{2a-1};\dfrac{3a}{2a-1}\right)\)
\(\Rightarrow MB^2=\left(\dfrac{2a+2}{2a-1}-1\right)^2+\left(\dfrac{3a}{2a-1}\right)^2=\dfrac{9a^2+9}{4a^2-4a+1}\left(2\right)\)
Đề MB = 3 MA
\(\Leftrightarrow MB^2=9MA^2\Leftrightarrow\dfrac{9a^2+9}{4a^2-4a+1}=\dfrac{9\left(4a^2+4\right)}{a^2+2a+1}\\ \Leftrightarrow a^2+2a+1=4\left(4a^2-4a+1\right)\Leftrightarrow15a^2-18a+3=0\\ \Leftrightarrow5a^2-6a+1=0\Leftrightarrow\begin{matrix}a=1\\a=\dfrac{1}{5}\end{matrix}\left(t.m\right)\\ \Leftrightarrow\begin{matrix}\left(d\right):y=x-1\\\left(d\right):y=\dfrac{1}{5}x-\dfrac{1}{5}\end{matrix}\)

Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D

Để hai đường song song thì m=2 và m-1=1 và m<>-1
=>m=2

Denta tạo với d1, d2 1 tam giác cân với đỉnh là giao điểm của d1, d2 khi và chỉ khi denta vuông góc phân giác tạo bởi d1, d2
Gọi \(A\left(x;y\right)\) là 1 điểm bất kì thuộc phân giác tạo bởi 2 đường thẳng d1, d2
\(\Rightarrow\dfrac{\left|x-7y+17\right|}{\sqrt{1^2+\left(-7\right)^2}}=\dfrac{\left|x+y-5\right|}{\sqrt{1^2+1^2}}\Leftrightarrow\left|x-7y+17\right|=\left|5x+5y-25\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+5y-25=x-7y+17\\5x+5y-25=-x+7y-17\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3y+\dfrac{21}{2}=0\\3x-y-4=0\end{matrix}\right.\)
\(\Rightarrow\Delta\) nhận \(\left(3;-1\right)\) hoặc \(\left(1;3\right)\) là 1 vtpt
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}3\left(x-0\right)-1\left(y-1\right)=0\\1\left(x-0\right)+3\left(y-1\right)=0\end{matrix}\right.\)

Đáp án B
+Giao điểm của d1 và d2 là nghiệm của hệ:
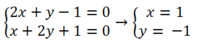
Vậy 2 đường thẳng d1 và d2 tại A( 1 ; -1) .
+Để 3 đường thẳng đã cho đồng quy thì d3 phải đi qua điểm A nên tọa độ A thỏa phương trình d3
Suy ra : m+ 1-7= 0 hay m= 6.
