Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Hai đường thẳng d 1 và d 2 có hai vectơ chỉ phương tỉ lệ (-2; 2; -4) = -2(1; -1; 2) và có điểm chung M(0; 1; 1)
Suy ra d 1 và d 2 trùng nhau.

Chọn D.
Đường thẳng d1 đi qua điểm M1(1;1;1) vectơ chỉ phương u 1 → 0 ; - 2 ; 1
Đường thẳng d2 đi qua điểm M2(1;0;1) vectơ chỉ phương u 2 → 1 ; 2 ; 2
![]()
Gọi n → là một vectơ pháp tuyến của mặt phẳng (P), ta có:

Mặt phẳng (P) đi qua điểm M1(1;1;1) và nhận vectơ pháp tuyến có phương trình:
-6(x - 1) + 1(y - 1) + 2(z - 1) = 0 hay – 6x + y + 2z + 3 = 0.

Đáp án B
Mặt cầu S : x - 1 2 + y + 1 2 + z 2 = 11 có tâm I(1;-1;0) bán kính R= 11
Các đường thẳng d 1 , d 2 có vectơ chỉ phương lần lượt là:
![]()
Mặt phẳng α song song với d 1 , d 2 có vectơ pháp tuyến là:
![]()
α có dạng: α : 3x-y-z+d=0. Vì α tiếp xúc với (S ) nên: d(I; α )=R
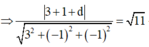
![]()
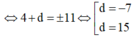
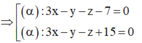
Nhận thấy điểm A(5;-1;1) ∈ d 1 cũng thuộc vào mặt phẳng 3x-y-z+15=0 =>mặt phẳng này chứa d 1
Vậy phương trình mặt phẳng α thỏa mãn yêu cầu bài toán là: α : 3x-y-z+7=0
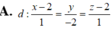
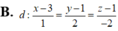
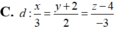

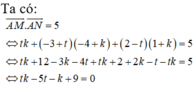

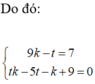


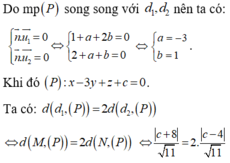
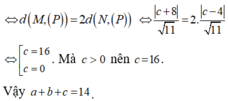





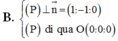
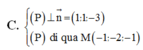
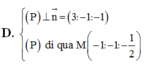
2 mp (P) và (Q) // với nhau.→vecto pháp tuyến của mp này cũng là vecto pt của mặt phẳng kia, tìm vecto pt của một trong hai mặt phẳng bằng cách tìm đoạn vuông góc chung của 2 đường thẳng d1 và d2.