Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, 2 đường thẳng // với nhau khi
\(\hept{\begin{cases}k+3=5-k\\2\ne3\end{cases}\Leftrightarrow k=1}\)
b, 2 đường thẳng cắt nhau khi
\(k+3\ne5-k\Leftrightarrow k\ne1\)
c, 2 đường thẳng trên ko thể trùng nhau được vì hệ số tự do 2 \(\ne\)3
Hàm số y = ( k + 1) x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = ( 3 – 2k ) x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là :
\(k+1\ne0\)và \(3-2k\ne0\)hay \(k\ne-1\)và \(k\ne\frac{3}{2}\)( * )
b) Hai đường thẳng y = ( k + 1 ) x + 3 và y = ( 3 – 2k ) x + 1 là hàm số bậc nhất nên \(a\ne0\) và \(a'\ne0\) Hai đường thẳng này cắt nhau khi \(a\ne a'\) tức là :
\(\hept{\begin{cases}k+1\ne0\\3-2k\ne\\k+1\ne3-2k\end{cases}0}\Leftrightarrow\hept{\begin{cases}k\ne-1\\2k\ne\\3k\ne2\end{cases}3}\Leftrightarrow\hept{\begin{cases}k\ne-1\\k\ne\\k\ne\frac{2}{3}\end{cases}\frac{3}{2}}\)
Với \(k\ne-1 ; k\ne\frac{3}{2} ; k\ne\frac{2}{3}\) thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do \(b\ne b'\) ( vì \(3\ne1\) ) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.

Hàm số y = ( k + 1)x + 3 có các hệ số a = k + 1, b = 3
Hàm số y = (3 – 2k)x + 1 có các hệ số a' = 3 - 2k, b' = 1
Hai hàm số là hàm số bậc nhất nên a và a' khác 0, tức là:
![]()
a) Theo đề bài ta có b ≠ b' (vì 3 ≠ 1)
Nên hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 song song với nhau khi a = a'
tức là: k + 1 = 3 – 2k
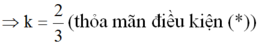
b) Hai đường thẳng y = (k + 1)x + 3 và y = (3 – 2k)x + 1 là hàm số bậc nhất nên a ≠ 0 và a' ≠ 0. Hai đường thẳng này cắt nhau khi a ≠ a' tức là:
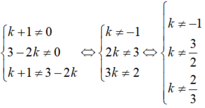
Vậy với ![]() thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
thì đồ thị của hai hàm số trên là hai đường thẳng cắt nhau.
c) Do b ≠ b' (vì 3 ≠ 1) nên hai đường thẳng không thể trùng nhau với mọi giá trị k.

1) Không thể trùng nhau vì b \(\ne\)b'
2)
a) song song khi \(\int^{m-1=3}_{2\ne-1}\Rightarrow m=4\)
b) cắt nhau a\(\ne\)a' => m\(\ne\)4
c) vuông góc với nhau khi a.a' =-1 =>3(m-1) =-1 => m-1 =-1/3 => m = 1 - 1/3 =2/3

a, y là hàm số bậc nhất khi \(2-m\ne0\Leftrightarrow m\ne2\)
b , y đồng biến khi 2 - m > 0 => m < 2
y nghịch biến khi 2 - m < 0 => m > 2
c, (d) // y=4-x khi
\(\hept{\begin{cases}2-m=4\\m-1\ne-x\end{cases}}\Leftrightarrow\hept{\begin{cases}m=-2\\m\ne-x+1\end{cases}}\Leftrightarrow m=-2\)
👍👍✔✔✔

a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4

\(a,\Leftrightarrow3m-1=m+3\Leftrightarrow2m=4\Leftrightarrow m=2\\ b,\Leftrightarrow3m-1\ne m+3\Leftrightarrow m\ne2\)
Phần a là m khác 0 nhé. Mình nhầm tí