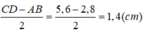Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
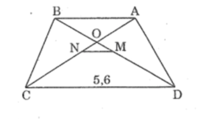
Vì ABCD là hình thang cân có AB // CD nên:
AC = BD (1)
Xét ΔADC và ΔBCD, ta có:
AC = BD (chứng minh trên)
AD = BC (ABCD cân)
CD cạnh chung
Suy ra: △ ADC = △ BCD (c.c.c)
Suy ra : ∠ (ACD) = ∠ ( BDC)
Hay ∠ (OCD) = ∠ ( ODC)
Suy ra tam giác OCD cân tại O
Suy ra: OD = OC (tính chất tam giác cân) (2)
Từ (1) và (2) suy ra: OA = OB
Ta có: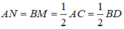 
Mà OA = OB ⇒ OM = ON
Lại có: MD = 3MO (gt) ⇒ NC = 3NO
Trong ΔOCD, ta có: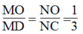 
Suy ra: MN // CD (Định lí đảo của định lí Ta-lét)
Ta có: OD = OM + MD = OM + 3OM = 4OM
Trong ΔOCD, ta có: MN // CD
Suy ra: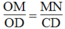 
Hệ quả định lí Ta-lét)
Suy ra: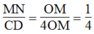 
Suy ra: MN = 1/4 CD = 1/4 .5,6 = 1,4 (cm)
Ta có: MB = MD (gt)
Suy ra: MB = 3OM hay OB = 2OM
Lại có: AB // CD (gt) suy ra: MN // AB
Ta có: MN // AB, áp dụng hệ quả định lý Ta – let ta được:
(Hệ quả định lí Ta-lét)
Suy ra: 
Vậy: AB = 2MN = 2.1,4 = 2,8(cm)
- Xét hình thoi \(ABCD\) ta có:
Hai đường chéo \(AC\) và \(BD\) cắt nhau tại \(O\) (gt).
\(\Rightarrow AC\perp BD\) tại \(O\).
-Ta có: \(\widehat{HAM}+\widehat{AMH}=90^0\)(\(\Delta AHM\) vuông tại \(H\)).
\(\widehat{BNH}+\widehat{OMN}=90^0\)(\(\Delta MON\) vuông tại \(O\))
Mà \(\widehat{AMH}=\widehat{OMN}\)(đôi đỉnh).
=>\(\widehat{HAM}=\widehat{BNH}\).
- Xét \(\Delta NBH\) và \(\Delta AMH\) ta có:
\(\widehat{BHN}=\widehat{AHM}=90^0\)..
\(\widehat{HAM}=\widehat{BNH}\) (cmt)
\(\Rightarrow\) \(\Delta NBH\) ∼\(\Delta AMH\) (g-g).
\(\Rightarrow\)\(\dfrac{BH}{HM}=\dfrac{HN}{AH}\)(2 tỉ lệ tương ứng).
\(\Rightarrow BH.AH=HN.HM\).
Mà \(AH=BH=\dfrac{1}{2}AB\) (\(H\) là trung điểm \(AB\)).
\(\Rightarrow\dfrac{1}{2}AB.\dfrac{1}{2}AB=HN.HM\)
\(\Rightarrow AB^2=4HM.HN\). \(\left(1\right)\)
- Xét \(\Delta ABO\) và \(\Delta AMH\) ta có:
\(\widehat{AOB}=\widehat{AHM}=90^0\)..
\(\widehat{A}\) là góc chung
\(\Rightarrow\) \(\Delta ABO\) ∼\(\Delta AMH\) (g-g).
\(\Rightarrow\)\(\dfrac{AO}{AH}=\dfrac{AB}{AM}\)(2 tỉ lệ tương ứng).
\(\Rightarrow AB.AH=AO.AM\).
Mà \(AH=\dfrac{1}{2}AB\) (\(H\) là trung điểm \(AB\)).
\(\Rightarrow AB.\dfrac{1}{2}AB=AO.AM\)
\(\Rightarrow AB^2=2HM.HN\) \(\left(2\right)\).
-Từ \(\left(1\right)\) và \(\left(2\right)\) suy ra: \(AB^2=4.HM.HN=2.AO.AM\)