Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

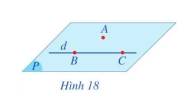
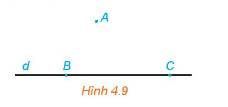
a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

thôi để giải luôn
Xét phương trình: \(x^3+ax^2+bx+c=0\left(1\right)\)
Đặt : \(f\left(x\right)=x^3+2x^2+bc+c\)
Từ giả thiết \(\left\{{}\begin{matrix}4a+c>8+2b\Rightarrow-8+4a-2b+c>0\Rightarrow f\left(-2\right)>0\\a+b+c< -1\Rightarrow1+a+b+c< 0\Rightarrow f\left(1\right)< 0\end{matrix}\right.\)
Do đó \(f\left(-2\right).f\left(1\right)< 0\) nên pt (1) có ít nhất một nghiệm trong \(\left(-2;1\right)\)
Ta nhận thấy:
\(\overset{lim}{x\rightarrow-\infty}f\left(x\right)=-\infty\) mà \(f\left(-2\right)>0\) nên phương trình (1) có ít nhất một nghiệm \(\alpha\in\left(-\infty;-2\right)\)
Tương tự: \(\overset{lim}{x\rightarrow+\infty}f\left(x\right)=+\infty\) mà \(f\left(1\right)< 0\) nên phương trình (1) có ít nhất một nghiệm \(\beta\in\left(1+\infty\right)\)
Như vậy phương trình đã cho có ít nhất 3 nghiệm thực phân biệt, mặt khác phương trình bậc 3 có tối đa 3 nghiệm nên pt trên sẽ có 3 nghiệm thực phân biệt.

Xét tập X = {A, B, C, D, E ; F}. Với mỗi cách chọn hai phần tử của tập X và sắp xếp theo một thứ tự ta được một vectơ thỏa mãn yêu cầu
Mỗi vectơ thỏa mãn yêu cầu tương ứng cho ta một chỉnh hợp chập 2 của 6 phần tử thuộc tập X.
Vậy số các vectơ thỏa mãn yêu cầu bằng số tất cả các chỉnh hợp chập 2 của 6, bằng
Chọn C.

Có \(C^2_4=6\left(đường\right)\) đi qua 2 điểm trong 4 điểm đã cho

\(\left(c;d\right)\Rightarrow\left(-c;-d\right)\)
\(\left(a-1\right)^2+\left(b-1\right)^2=1\)
\(\left(c-5\right)^2+\left(d-5\right)^2=100\)
Gọi \(A\left(a;b\right)\) thuộc đường tròn có pt \(\left(x-1\right)^2+\left(y-1\right)^2=1\) (C) có tâm \(I\left(1;1\right)\) bán kính \(R=1\)
\(B\left(d;c\right)\) thuộc đường tròn có pt \(\left(x-5\right)^2+\left(y-5\right)^2=100\) (C') có tâm \(I'\left(5;5\right)\) bán kính \(R=10\)
\(\Rightarrow AB^2=P=\left(a-d\right)^2+\left(b-c\right)^2\)
\(P_{min}\Leftrightarrow A;B\) là giao điểm nằm cùng phía so với I và I' của đường thẳng II' với 2 đường tròn
Phương trình II': \(x-y=0\)
\(\Rightarrow A\left(\dfrac{2-\sqrt{2}}{2};\dfrac{2-\sqrt{2}}{2}\right)\) ; \(B\left(5-5\sqrt{2};5-5\sqrt{2}\right)\)
\(\Rightarrow P_{min}=AB=\dfrac{9\sqrt{2}-8}{\sqrt{2}}=9-4\sqrt{2}\)

a)
Các phép biến hình lần lượt là: Phép tịnh tiến theo véc tơ \(\overrightarrow{0}\); Phép quay tâm A góc \(\phi\) bất kì; phép vị tự tâm A tỉ số k bất kì.
b)
Phép tịnh tiến theo véc tơ \(\overrightarrow{AB}\); Phép đối xứng tâm qua trung điểm của AB; Phép quay tâm I là trung điểm của AB và góc \(\phi=90^o\); Phép vị tự tâm A tỉ số \(k=AB\).
c)
Phép tịnh tiến theo một véc tơ bất kì; Phép đối xứng tâm có tâm đối xứng nằm trên đường thẳng d; Phép quay bất kì; Phép vị tự có tâm nằm trên đường thẳng d.

Mặt phẳng (ABC) chứa điểm A và đường thẳng d.
Do đó mp(ABC) cũng chứa hai đường thẳng AB và BC.
Ta có A B → = C D →
khi và chỉ khi AB= CD
Suy ra tập hợp các điểm D thỏa yêu cầu bài toán là đường tròn tâm C bán kính AB.
Chọn D