Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Do M thuộc d nên M( x; 2x+ 3)
Suy ra:
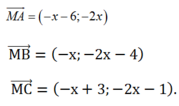
Do đó:
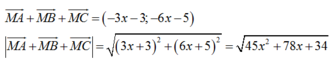
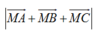
nhỏ nhất khi và chỉ khi: f(x) = 45x2+ 78x + 34 nhỏ nhất
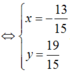

\(M\in\left(d\right)\Rightarrow M\left(a;a+6\right)\Rightarrow\left\{{}\begin{matrix}MA=\sqrt{\left(a-2\right)^2+\left(a+4\right)^2}=\sqrt{2\left(a+1\right)^2+18}\\MB=\sqrt{\left(a-3\right)^2+\left(a+6\right)^2}=\sqrt{2\left(a+\dfrac{3}{2}\right)^2+\dfrac{81}{2}}=\sqrt{2\left(-\dfrac{3}{2}-a\right)^2+\dfrac{81}{2}}\end{matrix}\right.\)
\(\Rightarrow MA+MB=\sqrt{\sqrt{2}^2\left(a+1\right)^2+18}+\sqrt{\sqrt{2}^2\left(-\dfrac{3}{2}-a\right)^2+\dfrac{81}{2}}\ge\sqrt{\left(\sqrt{2}.a+\sqrt{2}-\dfrac{3}{2}.\sqrt{2}-\sqrt{2}.a\right)^2+\left(\sqrt{18}+\sqrt{\dfrac{81}{2}}\right)^2}=\sqrt{\dfrac{1}{2}+\dfrac{225}{2}}=\sqrt{133}\)
\(dấu"="xayra\Leftrightarrow\dfrac{\sqrt{2}\left(a+1\right)}{\sqrt{18}}=\dfrac{\sqrt{2}\left(-\dfrac{3}{2}-a\right)}{\sqrt{\dfrac{81}{2}}}\Leftrightarrow a=-\dfrac{6}{5}\Rightarrow M\left(-\dfrac{6}{5};\dfrac{24}{5}\right)\)


Ta thấy \(\left(2-2+1\right)\left(1-0+1\right)=2>0\Rightarrow A,B\) khác phía so với \(\Delta\)
Lấy B' đối xứng với B qua \(\Delta\)
BB' có phương trình \(2x+y+m=0\)
Do B thuộc đường thẳng BB' nên \(m=-2\Rightarrow BB':2x+y-2=0\)
B' có tọa độ là nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+1=0\\2x+y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=\dfrac{4}{5}\end{matrix}\right.\Rightarrow B'=\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)
a, \(MA+MB=MA+MB'\ge AB'\)
\(min=AB'\Leftrightarrow M\) là giao điểm của AB' và \(\Delta\)
\(\Leftrightarrow...\)
b, \(\left|MA-MB\right|=\left|MA-MB'\right|\le AB'\)
\(max=AB'\Leftrightarrow M\) là giao điểm của AB' và \(\Delta\)
\(\Leftrightarrow...\)

Đường thẳng đi qua hai điểm A và B nhận \(\overrightarrow{AB}=\left(-2;-4\right)\) làm vecto chỉ phương.
Phương trình đường thẳng AB là \(\dfrac{x-1}{-2}=\dfrac{y-3}{-4}\Leftrightarrow2x-y+1=0\)
\(P=MA+MB\) đạt giá trị nhỏ nhất khi M, A, B thẳng hàng
\(\Leftrightarrow M\) là giao điểm của đường thẳng AB và d
\(\Leftrightarrow M\) có tọa độ nghiệm của hệ \(\left\{{}\begin{matrix}x-2y+3=0\\2x-y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow M\left(\dfrac{1}{3};\dfrac{5}{3}\right)\)

M thuộc d nên: \(a-2b-2=0\Rightarrow2b=a-2\)
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(-a;1-b\right)\\\overrightarrow{MB}=\left(3-a;4-b\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}=\left(3-2a;5-2b\right)=\left(3-2a;9-2a\right)\)
Đặt \(T=\left|\overrightarrow{MA}+\overrightarrow{MB}\right|=\sqrt{\left(3-2a\right)^2+\left(9-2a\right)^2}=\sqrt{8a^2-48a+90}=\sqrt{8\left(a-3\right)^2+18}\ge\sqrt{18}\)
Dấu "=" xảy ra khi \(a-3=0\Leftrightarrow a=3\Rightarrow b=\dfrac{1}{2}\)

a) Gọi E là trung điểm AB \(\Rightarrow\) \(\overrightarrow{IA}+\overrightarrow{IB}=2\overrightarrow{IE}\)
\(\overrightarrow{IA}+\overrightarrow{IB}+3\overrightarrow{IC}=\overrightarrow{0}\)
\(2\overrightarrow{IE}+3\overrightarrow{IC}=\overrightarrow{0}\)
A B C E I M d
b) \(\left|\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\right|\)
\(=\left|\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{MI}+\overrightarrow{IB}+3\overrightarrow{MI}+3\overrightarrow{IC}\right|\)
\(=5MI\)
\(\left|\overrightarrow{MA}+\overrightarrow{MB}+3\overrightarrow{MC}\right|min\Leftrightarrow MImin\)
\(\Leftrightarrow\) M là hình chiếu của I trên d
Đề kiểu gì mà cho điểm A nằm ngay trên đường thẳng d như vậy nhỉ?
Theo BĐT tam giác ta có:
\(MA+MB\ge AB\)
Dấu "=" xảy ra khi M, A, B thẳng hàng, hay M là giao điểm của AB và d
Nhưng do A nằm trên d nên giao điểm của AB và d chính là A
Vậy M trùng A, hay M có tọa độ \(M\left(3;4\right)\)
//Ko cần tính toán bất kì 1 bước nào hết, chỉ cần lý luận là có kết quả. Chắc người ra đề ko để ý đến chuyện điểm A bất ngờ nằm trên d.