Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mọi người làm nhanh jup mik nhé, ai có đáp án sẽ k luôn. Kamsa =)

Hướng dẫn làm bài:
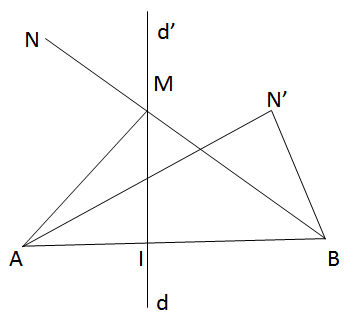
a) Vì M nằm trên d, d là trung trực của AB nên MA = MB (1)
Vì nên đoạn thẳng NB cắt d tại M suy ra M nằm giữa N và B.
Hay NM + MB = NB (2)
Từ (1) và (2) => NB = MA + NM
b) Gọi AN’ cắt d tại I
Trong tam giác N’IB có : N’B < IN’ + IB
Mà IA = IB (I thuộc trung trực của AB)
=> N’B < IN’ + NA => N’B < AN’
c) Vì LA < LB nên L không thuộc d, theo chứng minh câu b suy ra L thuộc PA.
a) Vì M nằm trên d, d là trung trực của AB nên MA = MB (1)
Vì nên đoạn thẳng NB cắt d tại M suy ra M nằm giữa N và B.
Hay NM + MB = NB (2)
Từ (1) và (2) => NB = MA + NM
b) Gọi AN’ cắt d tại I
Trong tam giác N’IB có : N’B < IN’ + IB
Mà IA = IB (I thuộc trung trực của AB)
=> N’B < IN’ + NA => N’B < AN’
c) Vì LA < LB nên L không thuộc d, theo chứng minh câu b suy ra L thuộc PA.

x y A B C M
Lấy M sao cho xy là trung trực của AM
điểm C thuộc xy => CA = CM => CA + BC = CM + BC
Theo bất đẳng thức tam giác, trong tam giác CBM có CM + BC \(\ge\) BM
=> AC + BC \(\ge\) BM
vậy AC + BC ngắn nhất = BM khi B; C; M thẳng hàng
=> C là giao của BM và đường thằng xy thì tổng AC + BC ngắn nhất

Trong số n đường thẳng đã vẽ, nhiều nhất là có một và chỉ một đường thẳng song song với xy. Do đó muốn có ít nhất 10 đường thẳng cắt xy thì số đường thẳng phải vẽ ít nhất là 11. Vậy n = 11.
Tính chất hai đường thẳng song song

BH vuong goc voi AM=>BH=<BM
CE vuong goc voi AM=>CE=<CM
=>BH+CE=<BM+CM
=>d=<BC
Dau bang xay ra khi BH=BM; CE=CM
=>AM vuong goc voi BC